Алгоритм вычисления ПХ операторным методом

a) Определяем независимые начальные условия. Так как до скачка напряжение на входе нулевое (рисунок 6.1), то начальное напряжение ёмкости и начальный ток конденсатора – нулевые:

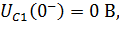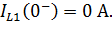
(6.38)

b) Формируем операторную схему замещения. При этом:

- источники энергии заменяем постоянными источниками, функции ЭДС которых являются изображениями по Лапласу исходных ЭДС. Для решаемой задачи, когда на входе – единичная ступенчатая функция σ₁(t), функция источника представится выражением

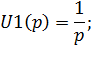
(6.39)

- индуктивности заменяются либо параллельной, либо последовательной схемами замещения (таблица 6.1).

На рисунке 6.13 – операторная схема замещения, полученная с учётом (6.38), (6.39).

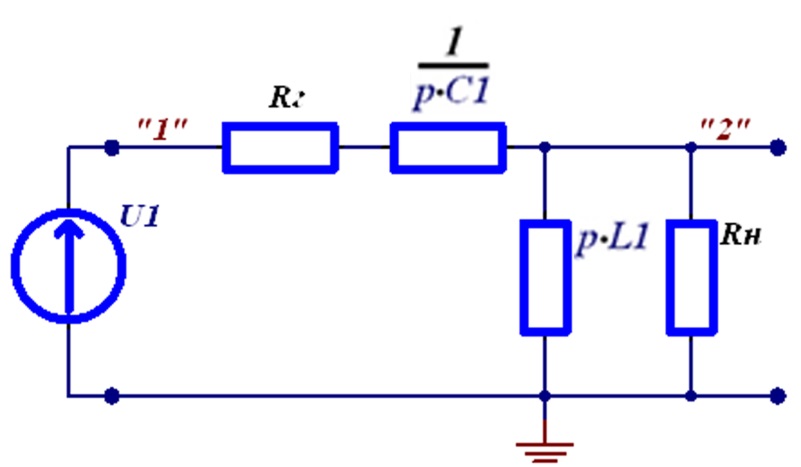
Рисунок 6.13 – Операторная схема анализируемой цепи

Таблица 6.1 – Операторные схемы замещения простейших элементов

Элемент	Схема замещения
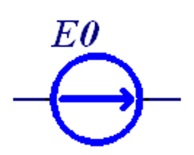
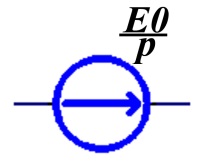
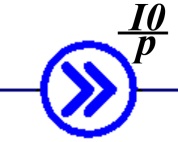
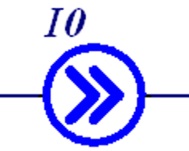Источники постоянных напряжения и тока
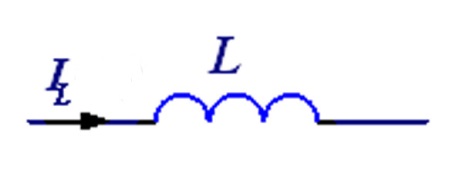
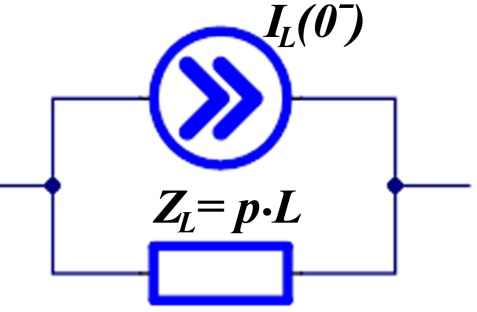	Параллельная
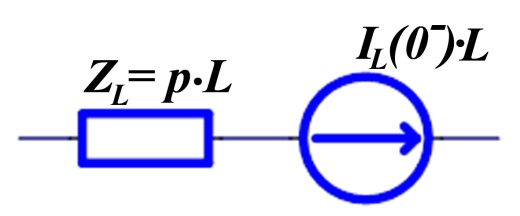Последовательная
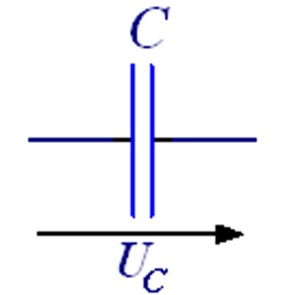
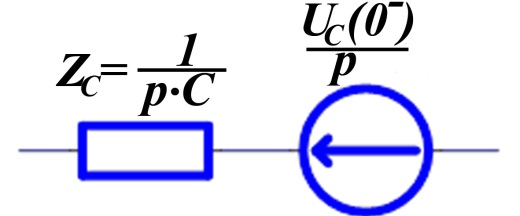	Последовательная
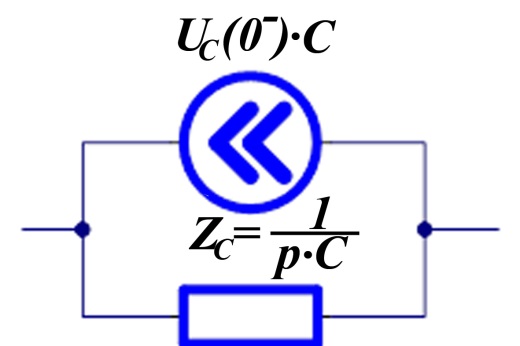Параллельная

c) Определение функции H1(p) изображения по Лапласу переходной характеристики. Указанная функция определяется любым удобным для вас методом расчёта резистивных цепей постоянного тока.

В курсовой работе мы можем воспользоваться передаточной функцией H(p), получаемой вами в подразделе 4.1. Так как

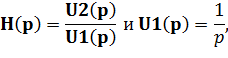
(6.40)

то

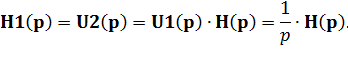
(6.41)

Для анализируемой схемы рисунка 6.2 или 6.12 передаточная функция 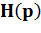полученав приложении A – выражение (А.7)

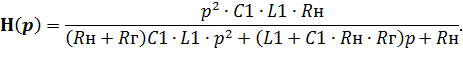
(6.42)

Подставляем (6.42) в (6.41) получим

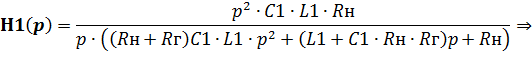
	(6.43)
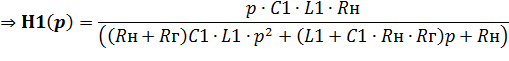
	(6.44)

d) Определение полюсов функции H1(p)– значений комплексной переменной p, при которой H1(p)→∞. Когда H1(p) имеет вид дробно рациональной функции, как и (6.44), её полюсами являются корни её полинома знаменателя

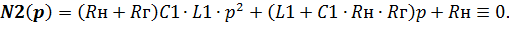
(6.45)

Для рассматриваемого примера этот полином совпадает с полиномом (6.5) знаменателя передаточной функции H(p), поэтому собственные частоты, полученные в пункте b) подраздела 6.2 (рисунок 6.7) и являются полюсами изображения переходной характеристики H1(p).

Однако не для всех вариантов курсовой переменная p знаменателя в произведении (6.41) сокращается при преобразованиях (6.43) – (6.44), полином знаменателя H1(p)может принять и вид

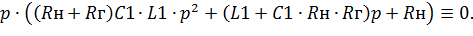
(6.46)

Тогда вы можете воспользоваться двумя вариантами решениями (6.46):

- вариант 1 – воспользоваться одним из инструментов программы MathCad для решения уравнений, описанных в пункте b) подраздела 6.2;

- вариант 2 – однако очевидно, что для уравнения (6.46) новым является только один корень

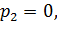
(6.47)

а остальные два совпадают с корнями полинома (6.5) или (6.45), так как выражение этого полинома совпадает с выражением в скобках для (6.46).

e) Вычисляем вычеты функции H1(p)

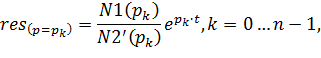
(6.48)

где N1(p) – полином числителя функции H1(p),

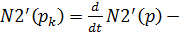производная полинома знаменателя функции H1(p),

p_k – k-й полюс: .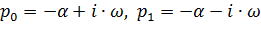

Для рассматриваемой цепи вводим в MathCad указанные полиномы

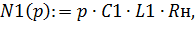
	(6.49)
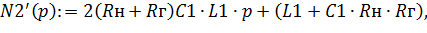
	(6.50)

Для вычетов (6.48) вычисляем коэффициенты перед экспонентами

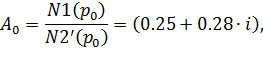
	(6.51)
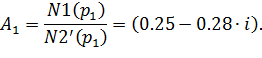
	(6.52)

Если в вычислениях не было ошибок, полученный результат совпадёт с подобными коэффициентами, вычисленными классическим методом – с результатом (6.32) пункта e) подраздела 6.2.

Ввод функции оригинала – функции ПХ в MathCfl выполняем так же, как и в пункте f) подраздела 6.2

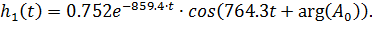
(6.53)