Метод наименьших квадратов
Запишем сумму квадратов отклонений (3) для всех точек 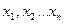 :
:
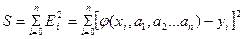 (4)
(4)
Параметры 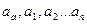 эмпирической формулы (2) будем находить из условий min функции
эмпирической формулы (2) будем находить из условий min функции 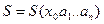 .В этом состоит метод наименьших квадратов.
.В этом состоит метод наименьших квадратов.
Поскольку здесь параметры 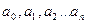 выступают в роли независимых функций S, то её min найдём приравнивая к нулю частные производные по этим переменным:
выступают в роли независимых функций S, то её min найдём приравнивая к нулю частные производные по этим переменным:
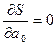
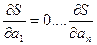 (5)
(5)
Полученные соотношения – системы управления для определения 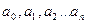
Рассмотрим применение метода наименьших квадратов для частного случая, широко используемых на примере. В качестве эмпирической формулы рассмотрим многочлен
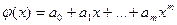 (6)
(6)
Формула (4) для определения суммы квадратов отклонений S примет вид
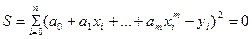 (7)
(7)
Для составления системы уравнений (5) найдем частные производные функции S=S( 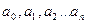 )
)
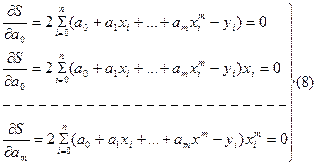
или 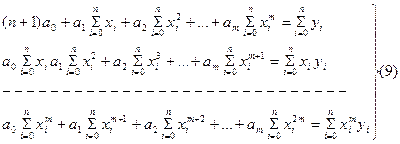
Решая последнюю систему относительно 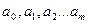 и получим многочлен (6)
и получим многочлен (6)
Систему (9) можно записать в более компактном виде
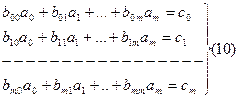
где 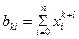
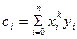
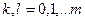 (m)
(m)
Лекция 17
Пример: метод наименьших квадратов для вывода эмпирической формулы, заданной в табличном виде:
Задана эмпирическая зависимость в табличной форме.
| x | 0,75 | 1,50 | 2,25 | 3,00 | 3,75 |
| y | 2,50 | 1,20 | 1,12 | 2,25 | 4,28 |
Найти зависимость y=f(x)
Решение
Если изобразить табличные значения на графике (1) то легко убедиться, что в качестве эмпирической формулы для аппроксимации функции y=f(x) можно принять параболу, т.е.

 квадратный трёхчлен
квадратный трёхчлен

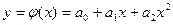
В данном случае m=2 n=4 и система (10) пример вид
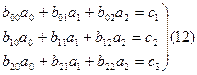
Коэффициенты этой системы могут быть вычислены по формулам (11) i=0,1,2,3,4
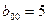
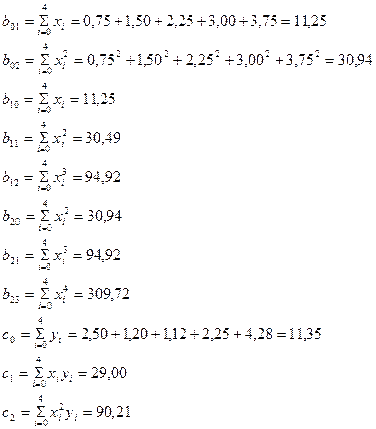
Система уравнений (12) запишем в виде
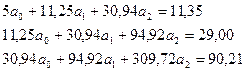
Отсюда находим параметры 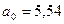
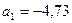
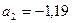 таким образом
таким образом 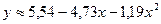 (13)
(13)
Оценим относительные погрешности полученной аппроксимации в заданных точках, т.е. найдем значение 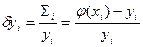 результаты вычисления представим в виде таблицы
результаты вычисления представим в виде таблицы
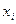
| 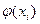
| 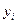
| 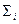
| 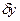
|
| 0,75 1,50 2,25 3,00 3,75 | 2,66 1,12 0,92 2,06 4,54 | 2,50 1,20 1,12 2,25 4,28 | 0,16 -0,08 -0,20 -0,19 0,26 | 0,064 -0,067 -0,179 -0,084 0,061 |
Пример Пусть на основании эксперимента получим значения функции y=f(x), которые записаны в таблицу
| x | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
| y | 0,31 | 0,82 | 1,29 | 1,85 | 2,51 | 3,02 |
С помощью метода наименьших квадратов функцию y=f(x) аппроксимировать линейной функцией 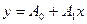
Решение Составим систему для определения 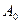 и
и 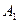
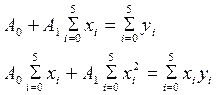
Дата добавления: 2016-07-27; просмотров: 2476;











