Метод конечных разностей решение краевых задач ОДУ.

Пусть дана краевая задача ОДУ

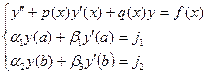
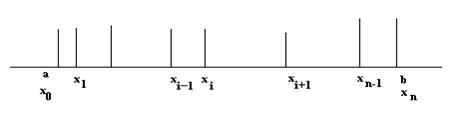
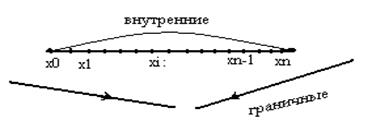
Требуется решить такое уравнение. Отрезок [a, b] разбивается точками на равные части x_j=x₀+jh. Точки разделяются на внутренние 1 ≤ j ≤ n-1 и граничные j=0 и j=n. Затем производные входящие в уравнение (1) 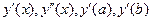заменяются в точках х_i приближенными конечно-разностными соотношениями.

y`(x_i)= 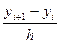~0(h) (*)

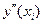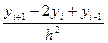= ~0(h²)

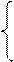
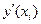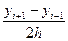= ~0(h²)

И подставим равенства (*0 в уравнение (1), получим

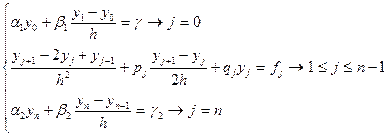(2)

Преобразуем (2) к виду (3), получишь

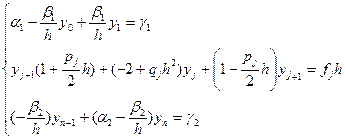(3)

c₀ y₀- b₀ y₁…………………..=f₀ j=0

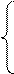(4) ……-a_j y_j-1+c_j y_j-b_j y_j+1….......=f_j 1≤ j≤ n-1

………………...-a_n y_n-1+c_ny_n=f_n j=n

Или

=

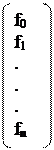
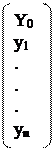
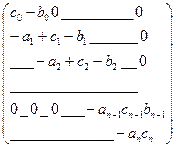Полученную систему решаем методом прогонки, которую мы рассматривали в системах линейных уравнений.

Лекция 10

Сплайны.

Пусть есть функция f(x) заданная в узлах отрезка [a,b]. Пусть заданны узлы интерполяции x₀x₁…x_n x_i 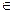[a,b] в которых заданны значения функции f(x₀) f(x₁)… f(x_n) [x₀x₁], [x₁x₂]… [x_n-1x_n]~∆- разбиения.

Будем приближать функцию f(x) на каждом отрезке ∆~[x_j-1x_j] полиномом

P_j,m(x)=a_0j+a_1jx+…+ a_njx^m

Сплайном назовем S_∆(x) функцию совпадающую на каждом участке [x_j-1x_j] с полиномом P_j,m(x) и такую, что во всех внутренних узлах непрерывную вместе со своими производными до (m-1) порядка включительно во всех точках x_i i=1, n-1.

Кубический сплайн.

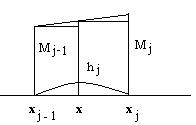
Будем считать, что на каждом участке [x_j-1x_j] мы приближаем полином 3=ей степени.

P_j,3(x)=ax³+bx²+cx+d, тогда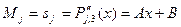

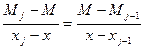
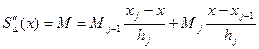(1)

Найдем S_∆(x) для чего проинтегрируем дважды (1), получим

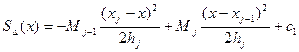
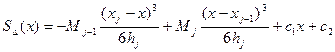
Найдем с₁ и с₂ из условия S_∆(x_j-1)= y _j-1 S_∆(x_j)= y _j

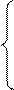
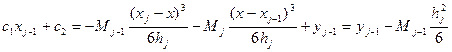
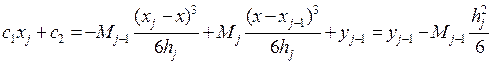
C₁h_j=y_j- M_j 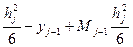=> C₁h_j=y_j-y_j-1+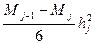

C₁=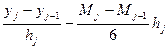

C₂=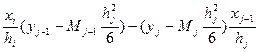

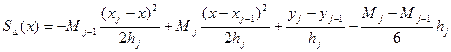
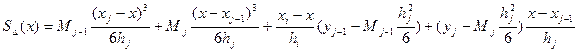
Поскольку S_∆^`(x_j-0)= S_∆(x_j+0)

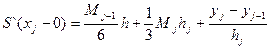
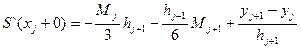
Приравнивая получаем

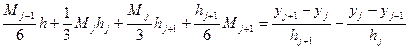(2)

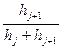λ_j= μ_i= 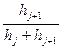λ_j+ μ_i=1

μ_iM_j-1+2M_j+ λ_j M_j=d_j j=1,n-1

Полученная система служит для определения M₀ M₁… M_n, подставляя в формулы (х) и (х^*) получим, что полином удовлетворяет 3-м свойствам

1) S_∆(x_j-0)= S(x_j+0)

2) S<sup>`</sup>(x<sub>j</sub>-0)= S` (x_j+0)

3) S^{``</sup>(x<sub>j</sub>-0)= S<sup>``}(x_j+0)

Лекция 11