Обусловленность систем линейных уравнений число обусловленности.

Задача над плохо обусловленной, если вычисляемые величины X очень чувствительны к небольшим изменениям исходных данных. Рассмотрим причины, определяющие решения X систем Ax=U (1)

Изменим правую часть U на U+δU, это приведет к изменениям решения x на x+δx и при постоянной матрице A, имеем:

A(x+ δx) = U+δU (2)

Из (1) (3)

Из (2) имеем Aδx=δUàδx=A^-1δU=> 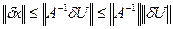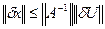(4)

Перемножим (3) и (4) получим

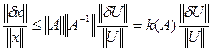(5)

Число k(A)= 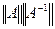называют числом обусловленности. Если число k(A) велико, то для большинства правых частей решение ненадежно. Это же число может быть использовано и для других задач. Пусть, например, δх – погрешность вызвана погрешностью δА элементов матрицы А, а правые части заданны точно, тогда имеем

(A+ δA)( x+ δx)=U

Из (1) имеем x=A^-1U (6)

x+ δx= (A+ δA) ^-1U (6a)

A^-1U+ δx= (A+ δA) ^-1U=> δx= [(A+ δA) ^-1- A^-1]U=> (7)

(A+ δA) ^-1- A^-1=[I- A^-1 (A+ δA) ] (A+ δA) ^-1=-A^-1δA(A+δA)^-1

Подставляя в (7) получим

δx=-A^-1δA(A+ δA) ^-1U

δx=-A^-1δA( x+ δx)

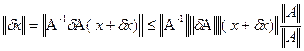
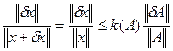(8)

Число обусловленности обладает рядом свойств

1) k(CA)=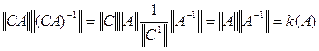

2) k(A)=k(A^-1)

3) k(A)= 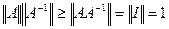k(A)≥1

4) Если m-min значение матрицы; M-max значение матрицы, то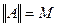

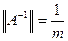и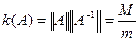

Отсюда следует наличие малого собственного значения матрицы А обязательно означает её плохую обусловленность. Однако матрица А может быть плохо обусловленной, когда у неё нет малого собственного значения. Например, наименьшее собственное значение матрицы 100^го порядка

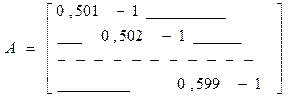
Равен m=0,501. Если же рассмотреть систему Ax=U c 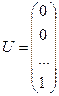, где , то имеем

То получим

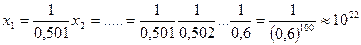
Первая компонента решения Ax=U система больше, чем 10²², т.е.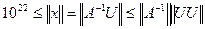

Отсюда

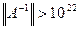
В свою очередь для любой матрицы

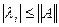и следовательно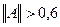

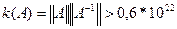
Матрица плохо обусловлена

Пример

Рассмотрим систему

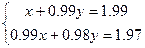
Точное решение x=1 и y=1

В рассматриваемом примере матрица системы AX=U симметрична и имеет собственное значение

m=0,00005

M=1,98005

Здесь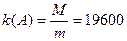

Система плохо обусловлена, а значит следует ожидать, что малые значения (сдвиг) правых частей приведут к большому изменению решения

, т.е. рассмотрим систему

x+0, 99y=1, 989903

0, 99x + 0,98y=1,970106

То получим решение x=3,000 y=-1,0203, т.е.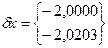

Здесь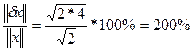

Значит небольшое изменение δU влечет за собой изменение относительной погрешности вычислительных величин 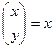на 200%. Задача плохо обусловлена.

Лекция 14