Приведение систем к виду, допускающему применение метода простых итераций.

Обычно система линейных уравнений задана в виде

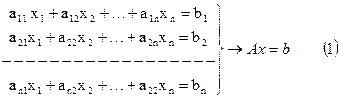
и для приведения её к виду x=Bx+b, допускающего применение метода простых итераций. Подбирают невырожденную матрицу H (det H≠0), так чтобы

Ax=b => HAx= Hb=> x- x+ HAx= Hb=>

X= x- HAx +V=> x= (I-HA)x+ V

Берем B=I-HB

Тогда получаем x= Bx+ V, причем

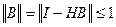
Матрицу H целесообразно близко к A^-1 так, чтобы HA~I. Так, например, если в матрице A вдоль главной диагонали элементы преобладают над остальными, то берут

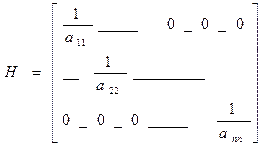
Если матрица A=A^* самосопряженная и положительно определенная A^*=A и λ у матрицы A положительна, у которой известны её max и min собственные значения.

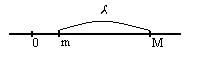
0≤ m≤M, то полная H= tI получим

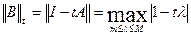
Т.к. надо найти 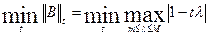, то

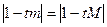
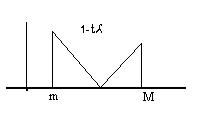
1) -(1-tm)=-(1-tM)

2) 1-tm=1-tM

3) -(1-tm)=(1-tM)

4) 1-tm=-(1-tM)

(3) и (4) 1-tm=-(1-tM)=>2=t(M+n)=>t=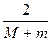

(1) и (2) 1-tm=1-tM=> t(M-m)=0 t=0 это не берем

Тогда

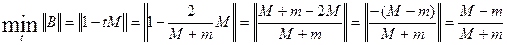
х^*= Bx^*+b

x^k= Bx^k-1+b

x^*-x^k=B(x^*-x^k-1)=BB(x^*-x^k-2)=…=B^k(x^*-x⁰)

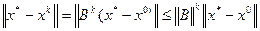
Получим max скорость сходимости

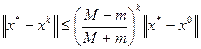
Пример простой итерации решить систему

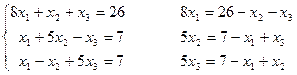
Пример

Приведем систему к нормальному виду x=Bx+V

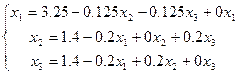
x=Bx+ V

=

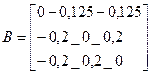
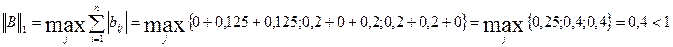Метод простой итерации сходится за

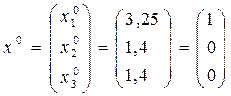
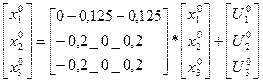
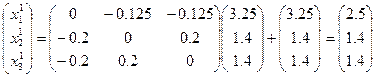
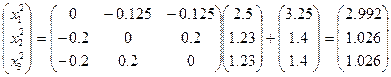
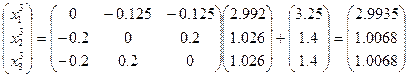
Тогда x₁=2,9935 x₂=1,0068 x₃=1,0068

Или x₁≈3 x₂≈1 x₃≈1

Метод Зейделя.

Решение системы Ax=U по методу Зейделя производится по формулам

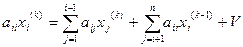
Если при вычислении i-той координаты вектора

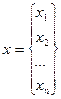
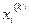учитывается найденные заранее уже координаты …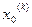

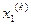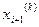
То вычисления будут проходить по формулам Зейделя.

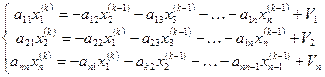
Лекция 13