Задача об эффективности рекламы.

Допустим, реализуется продукция, о которой на момент t из числа потенциальных покупателей N знает лишь х человек. Для ускорения сбыта продукции даны рекламные объявления. После этого информация о продукции распространяется среди покупателей посредством общения друг с другом.

С момента объявления рекламы число оповещенных покупателей есть функция времени 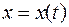. Эту функцию составить сложно, но понятно, что скорость оповещения потенциальных покупателей пропорциональна числу покупателей, знающих о товаре ( 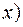, и числу покупателей, о нём ещё не знающих ( 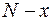). То есть

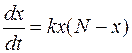, (1.3.)

где 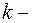коэффициент пропорциональности, характеризующий эффективность рекламы.

Решая данное уравнение, получаем:

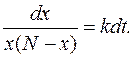
Интегрируем обе части :

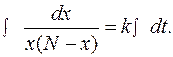
Находим левый интеграл, выразив дробно-линейную функцию через простейшие дроби (метод неопределенных коэффициентов):

=

.

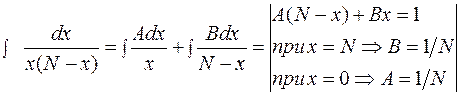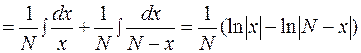Получили: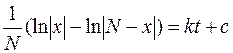

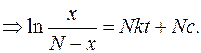
Обозначаем: 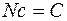, так как 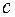- произвольное число.

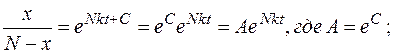
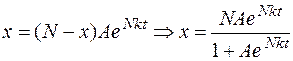- общее решение дифференциального уравнения (2.1.). Частное решение этого уравнения получим, зная число оповещенных рекламой на момент t = 0.

1.2.2. Задача о спросе и предложении.

Одним из экономических законов товарного производства является закон спроса и предложения, который заключается в единстве спроса и предложения и их объективном стремлении к соответствию.

Если бы была известна зависимость цены во времени на сезонный продукт 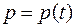, то производная от цены (тенденция формирования цены): 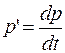. Тогда спрос (q) и предложение (p)можно представить линейными функциями:

;

,

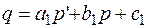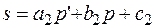где 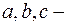коэффициенты, характеризующие данный продукт и рынок.

Чтобы спрос соответствовал предложению должно выполняться равенство .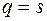

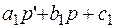
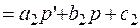
или -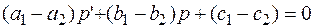

дифференциальное уравнение первого порядка. Решив его, находим зависимость 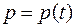, то есть стратегию изменения цены для сохранения соответствия между спросом и предложением.