N-канальная СМО с отказами (задача Эрланга)
Это одна из первых задач теории массового обслуживания. Она возникла из практических нужд телефонии и была решена в начале 20 века датским математиком Эрлангом.
Пусть в системе имеется n каналов, на которые поступает поток заявок с интенсивностью l. Поток обслуживаний имеет интенсивность m. Заявка, заставшая систему занятой, сразу же покидает ее.
Требуется найти абсолютную и относительную пропускную способность СМО; вероятность того, что заявка, пришедшая в момент времени t, получит отказ; среднее число заявок, обслуживаемых одновременно (среднее число занятых каналов).
Состояние системы S (СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов):
- S0 – в СМО нет ни одной заявки;
- S1 – в СМО находится одна заявка (один канал занят, остальные свободны);
- S2 – в СМО находится две заявки (два канала заняты, остальные свободны);
- . . .
- Sn – в СМО находится n заявок (все n каналов заняты).
Граф состояний СМО представлен на рис. 4.6.
Из состояния S0 в состояние S1 систему переводит поток заявок с интенсивностью l (как только приходит заявка, система переходит из S0 в S1). Если система находилась в состоянии S1 и пришла еще одна заявка, то она переходит в состояние S2 и т. д.

Рис. 4.6. Граф состояний N-канальной СМО с отказами
Пусть система находится в состоянии S1 (работает один канал). Он производит m обслуживаний в единицу времени. Поэтому дуга перехода из состояния S1 в состояние S0 нагружена интенсивностью m. Пусть теперь система находится в состоянии S2 (работают два канала). Чтобы ей перейти в S1, нужно, чтобы закончил обслуживание первый канал, либо второй. Суммарная интенсивность их потоков равна 2m и т. д.
Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом.
Абсолютная пропускная способность
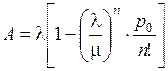 , шт/ед. времени,
, шт/ед. времени,
где n – количество каналов СМО; р0 – вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянии S0).
Для того, чтобы написать формулу для определения р0, рассмотрим рис. 4.7. Граф, представленный на рисунке, называют еще графом состояний для схемы «гибели и размножения».

Рис. 4.7. Граф состояний для схемы «гибели и размножения»
Вероятность того, что СМО находится в состоянии S1, когда один канал занят
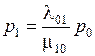 .
.
Вероятность того, что СМО находится в состоянии S2, т.е. когда два канала заняты
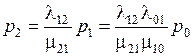 .
.
Вероятность того, что СМО находится в состоянии Sn, т.е. когда все каналы заняты
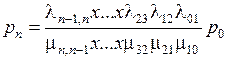 .
.
Вероятность нахождения СМО в начальном состоянии р0
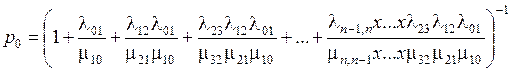 .
.
Применительно к n-канальной СМО с отказами
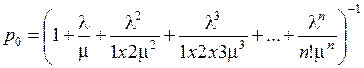 .
.
При этом 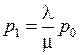 ;
; 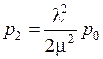 ;
; 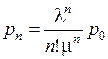 .
.
Относительная пропускная способность
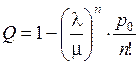 .
.
Абсолютная пропускная способность А = lQ.
Вероятность отказа
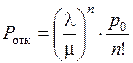 .
.
Среднее число занятых каналов (среднее число заявок, обслуживаемых одновременно)
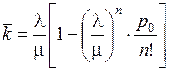 .
.
При этом 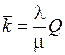 .
.
Пример № 1. Имеется технологическая система (участок), состоящая из трех одинаковых станков. В систему поступают для обработки детали в среднем через 0,5 часа ( 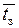 ). Среднее время изготовления одной детали
). Среднее время изготовления одной детали 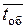 = 0,6 ч. Если при поступлении заявки на изготовление детали все станки заняты, то деталь направляется на другой участок таких же станков. Необходимо найти финальные вероятности состояний системы и характеристики (показатели эффективности) данной СМО.
= 0,6 ч. Если при поступлении заявки на изготовление детали все станки заняты, то деталь направляется на другой участок таких же станков. Необходимо найти финальные вероятности состояний системы и характеристики (показатели эффективности) данной СМО.
Интенсивность потока заявок
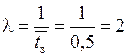 ,
,
т. е. в среднем две заявки на обработку деталей в час.
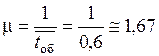 .
.
Граф состояний системы представлен на рис. 4.8.
Рис. 4.8
Возможные состояния системы: S0 – в СМО (на участке) нет ни одной заявки; S1 – в СМО (на участке) одна заявка; S2 – в СМО (на участке) две заявки; S3 – в СМО (на участке) три заявки (заняты все три станка).
Вероятность того, что все станки свободны:
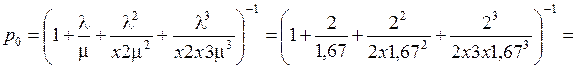
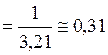 .
.
Вероятность того, что один станок занят
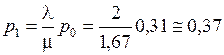 .
.
Вероятность того, что два станка заняты
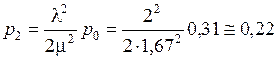 .
.
Вероятность того, что все три станка заняты
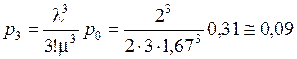 .
.
Абсолютная пропускная способность
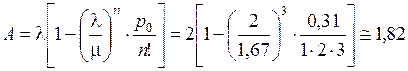 дет./ч.
дет./ч.
Относительная пропускная способность
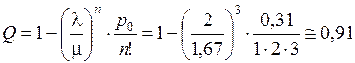 ;
;
Вероятность отказа
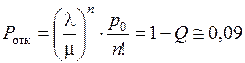 .
.
Среднее число занятых каналов (станков)
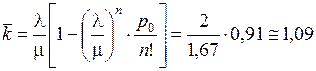 .
.
Таким образом, в среднем в этой системе обрабатывается 1,82 дет./ч (примерно 91 % направляемых деталей), при этом примерно 9 % деталей направляется для обработки на другие участки. Одновременно в среднем работает в основном один станок ( 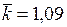 ). Но из-за случайных характеристик потока заявок иногда работают одновременно все три станка (рз = 0,09), отсюда 9 % отказов.
). Но из-за случайных характеристик потока заявок иногда работают одновременно все три станка (рз = 0,09), отсюда 9 % отказов.
Пример № 2. Пусть 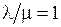 , Ротк £ 0,03 (т. е. £ 3 %). Найти оптимальное число каналов nопт, обеспечивающее минимум затрат на систему, при условии достижения требуемого уровня ее безотказной работы.
, Ротк £ 0,03 (т. е. £ 3 %). Найти оптимальное число каналов nопт, обеспечивающее минимум затрат на систему, при условии достижения требуемого уровня ее безотказной работы.
Целевая функция (затраты на СМО) запишется:
y = cn ® min,
где c – постоянная величина.
Решение:
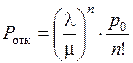 ;
; 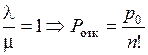
Ротк £ 0,03 Þ 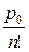 £ 0,03 Þ
£ 0,03 Þ 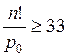 .
.
По другому можно записать:
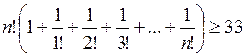 .
.
Последнее равенство начинает выполняться при nопт = 4, т. к.
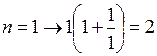 < 33;
< 33; 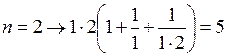 < 33;
< 33;
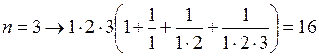 < 33;
< 33;
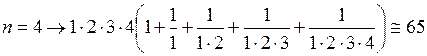 > 33.
> 33.
Пример № 3. Для условий предыдущей задачи определить оптимальное число каналов, обеспечивающее максимум прибыли от эксплуатации СМО в единицу времени.
Содержание каждого канала в единицу времени обходится в какую-то сумму. Чем больше каналов, тем больше затраты на эксплуатацию СМО. Вместе с тем, чем больше каналов (при l и m = const), тем больше доля обслуживаемых заявок. А каждая обслуженная заявка дает определенный доход в единицу времени. При увеличении числа каналов растут доходы D и расходы на эксплуатацию R. Чтобы решить эту задачу, необходимо найти оптимальное число каналов nопт, обеспечивающее максимум целевой функции P = D – R ® max, т. е. нужно максимизировать прибыль в единицу времени.
Дата добавления: 2018-11-26; просмотров: 1668;











