Дифференциальные уравнения с разделяющимися переменными.
Дифференциальное уравнение 1-го порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде: 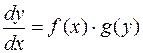 (2.3.)
(2.3.)
или в виде: 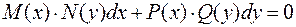 (2.4.)
(2.4.)
где 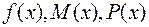 - некоторые функции переменной
- некоторые функции переменной 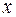 , а
, а 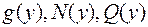 - функции переменной
- функции переменной 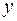 .
.
Для решения уравнений (3.3.) и (3.4.) их следует преобразовать так, чтобы функция и дифференциал переменной 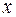 оказались в одной части уравнения, а функция и дифференциал переменной
оказались в одной части уравнения, а функция и дифференциал переменной 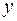 - в другой части. Затем следует проинтегрировать обе части полученного равенства.
- в другой части. Затем следует проинтегрировать обе части полученного равенства.
Так, уравнение вида 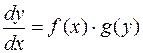 преобразуем к виду
преобразуем к виду
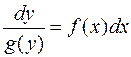
Далее интегрируем обе части: 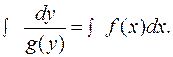
Уравнение 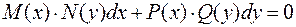 преобразуем к виду:
преобразуем к виду:
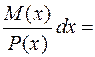
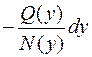
Далее интегрируем обе части: 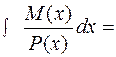
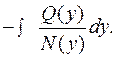
ПРИМЕР 2.1. Решить дифференциальное уравнение 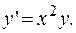
РЕШЕНИЕ.
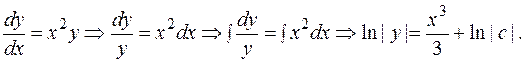
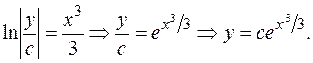 - общее решение.
- общее решение.
Заметим, что произвольную постоянную с можно брать в любом виде, удобном для дальнейших вычислений.
ПРИМЕР 2.2. Решить дифференциальное уравнение 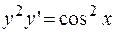 .
.
РЕШЕНИЕ.
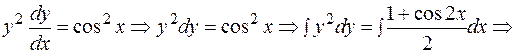
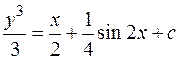 - общий интеграл.
- общий интеграл.
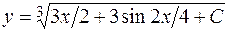 - общее решение, где
- общее решение, где 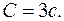
ПРИМЕР 2.3. Решить задачу Коши для уравнения 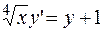 ,
,
если 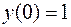 .
.
РЕШЕНИЕ.
Находим общее решение: 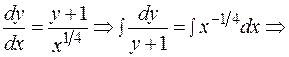
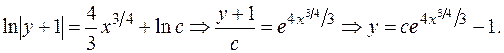
Находим частное решение, подставляя значения 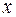 =0,
=0, 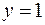 в общее решение:
в общее решение: 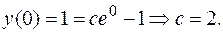
Таким образом: 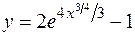 - частное решение для заданных начальных условий.
- частное решение для заданных начальных условий.
ПРИМЕР 2.4. Решить дифференциальное уравнение
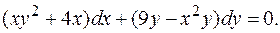
РЕШЕНИЕ.
Преобразовываем уравнение и разделяем переменные: 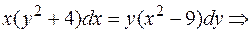
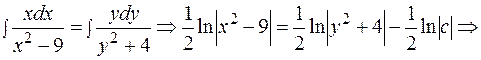
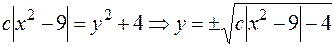 .
.
Дата добавления: 2020-10-25; просмотров: 666;











