Однородные дифференциальные уравнения 1-го порядка.

Дифференциальное уравнение 1-го порядка называется однородным, если оно может быть приведено к виду 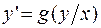, (2.9.)

где 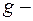функция переменной 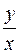, которую заменяют на .

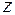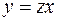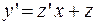Тогда: и . (2.10.)

Исходное уравнение принимает вид: .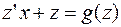

Далее: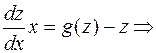

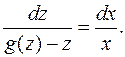
Заметим, что "однородным" называют линейное уравнение, в котором свободный член равен нулю. Для дифференциального уравнения понятие однородности имеет иной смысл. Функция 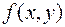называется однородной степени 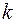(по переменным 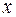и 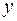), если для произвольного числа 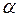выполняется равенство

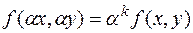. (2.11.)

Другими словами, каждое слагаемое функции имеет одну и ту же степень с учетом обеих переменных.

Например, функция 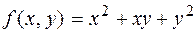является однородной, так как .

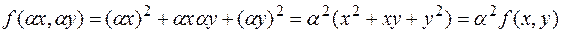ПРИМЕР 2.8. Решить дифференциальное уравнение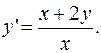

РЕШЕНИЕ. Преобразуем уравнение и получаем однородное дифференциальное уравнение. 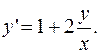Заменяем: .

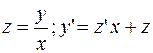Получили 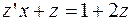- уравнение с разделяющимися переменными.

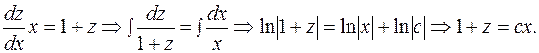
Возвращаемся к первоначальным переменным

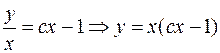- общее решение.

ПРИМЕР 2.9. Решить дифференциальное уравнение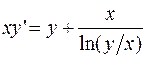

РЕШЕНИЕ. Делим обе части уравнения на 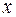и получаем однородное дифференциальное уравнение .

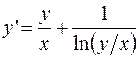Замена: 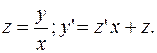Получаем: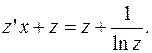

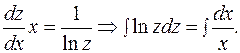Левый интеграл берем "по частям".

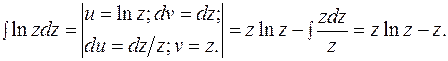
Получаем: 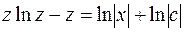. Выполняем обратную замену:

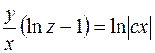- общий интеграл.