Дифференциальные уравнения вида
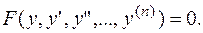 (3.4.)
(3.4.)
Данное дифференциальное уравнение не содержит переменной 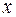 . Порядок уравнения можно понизить на единицу заменой:
. Порядок уравнения можно понизить на единицу заменой:
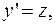 где
где 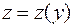 ;
; 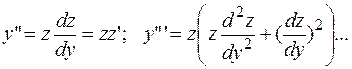 (3.5.)
(3.5.)
Эти производные находят по правилу дифференцирования сложных функций.
ПРИМЕР 3.5. Решить дифференциальное уравнение 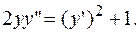
РЕШЕНИЕ. Полагаем 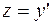 , тогда
, тогда 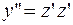 . Выполнив замену, получаем уравнение:
. Выполнив замену, получаем уравнение: 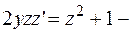 дифференциальное уравнение первого порядка с разделяющимися переменными.
дифференциальное уравнение первого порядка с разделяющимися переменными.
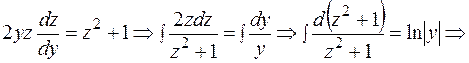
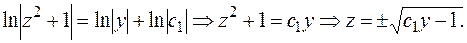
Выполняем обратную замену: 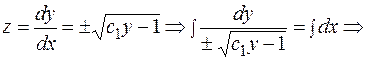
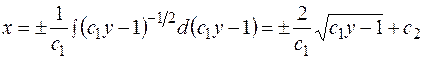 - общее решение, в котором
- общее решение, в котором 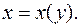
Дифференциальные уравнения вида
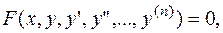 (3.6.)
(3.6.)
однородное относительно 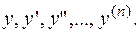
Порядок данного дифференциального уравнения можно понизить на единицу заменой 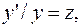 (3.7.)
(3.7.)
где 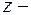 новая зависимая переменная. Тогда
новая зависимая переменная. Тогда
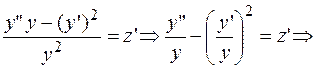
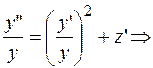
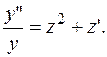 (3.8.)
(3.8.)
ПРИМЕР 3.6. Решить дифференциальное уравнение
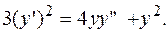
РЕШЕНИЕ. Делим обе части уравнения на 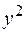 и получаем однородное дифференциальное уравнение второго порядка.
и получаем однородное дифференциальное уравнение второго порядка.
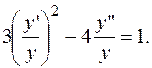
Полагаем: 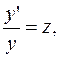
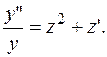
Выполнив замену, получаем уравнение: 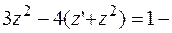 дифференциальное уравнение первого порядка с разделяющимися переменными.
дифференциальное уравнение первого порядка с разделяющимися переменными.
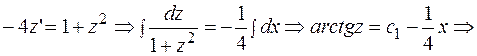
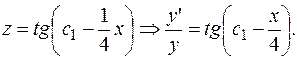 Интегрируя последнее уравнение, получаем:
Интегрируя последнее уравнение, получаем: 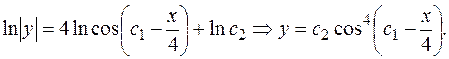
Дата добавления: 2020-10-25; просмотров: 593;











