ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШЕГО ПОРЯДКА. 3.1.Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
Внекоторых случаях решение дифференциальных уравнений высшего порядка может быть сведено к последовательному решению дифференциальных уравнений 1-го порядка. В этом случае говорят, что данное дифференциальное уравнение допускает понижение порядка.
Рассмотрим способы решения дифференциальных уравнений высшего порядка некоторых видов.
3.1.1. Дифференциальные уравнения вида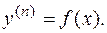 
(3.1.)
Уравнение не содержит переменной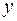 
и её производных более низкого порядка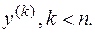 
Такое дифференциальное уравнение решается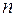 
- кратным интегрированием.
Так, для уравнений второго порядка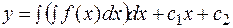 
.
ПРИМЕР 3.1. Решить дифференциальное уравнение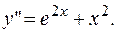 
РЕШЕНИЕ. Дважды интегрируем правую часть.
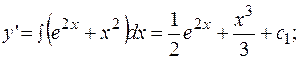
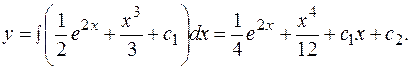- общее решение.
ПРИМЕР 3.2. Найти частное решение дифференциального уравнения
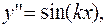удовлетворяющее начальным условиям: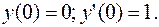 
РЕШЕНИЕ. Находим общее решение.
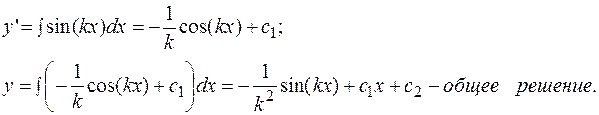
Находим частное решение по начальным условиям.
;
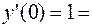
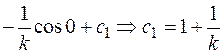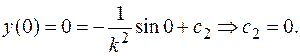
Частное решение: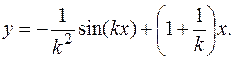 
Заметим, что это же уравнение можно решить и так:
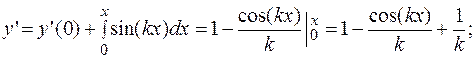
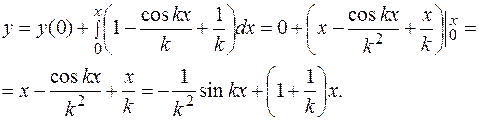
ПРИМЕР 3.3. Найти частное решение дифференциального уравнения
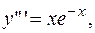удовлетворяющее начальным условиям: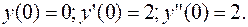 
РЕШЕНИЕ. Применим метод, рассмотренный в последнем примере.
= 
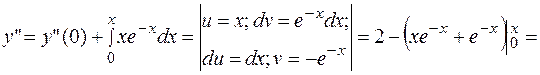
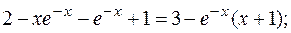
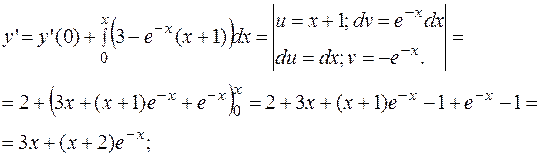
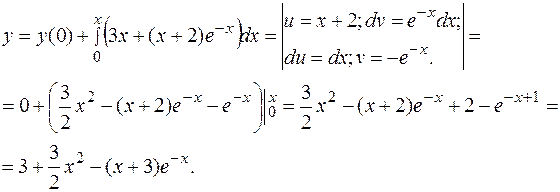
Дата добавления: 2020-10-25; просмотров: 574;
Поиск по сайту
Узнать еще
- А. Уравнения движения точки в декартовых координатах
- Абсолютные и дифференциальные вихретоковые преобразователи
- Автономные системы, символические уравнения Вопрос 2
- Алгебраические и трансцендентные уравнения
- Алгоритм составления уравнения химической реакции
- Анализ качества эмпирического уравнения множественной
- Анализ уравнения Ленгмюра
- Анализ уравнения Михаэлиса-Ментен
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по географии
Публикации по медицине
