Линейные дифференциальные уравнения 1-го порядка.
Дифференциальное уравнение 1-го порядка называется линейным, если оно имеет вид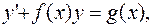 
(2.12.)
где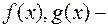 
некоторые непрерывные функции от переменной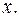 
Такие уравнения обычно решаются методом Бернулли. При этом выполняется замена: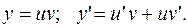 
(2.13.)
Тогда получаем: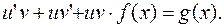 
Далее группируют второе и третье слагаемые: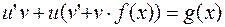 
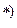и находят такое частное решение 
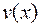, которое обращает выражение в скобках в ноль.
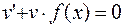
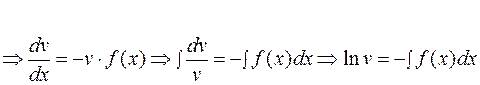
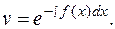
Заметим, что произвольную постоянную "с" здесь не записывают.
Решение 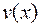подставляют в уравнение, помеченное знаком 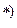, и находят переменную 
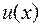, в которую записывают произвольную постоянную "с".
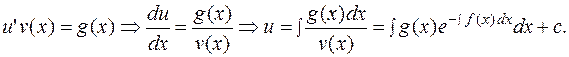
Затем составляют решение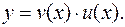 
ПРИМЕР 2.10. Решить дифференциальное уравнение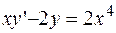 
.
РЕШЕНИЕ. Разделив обе части на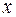 
, получаем линейное дифференциальное уравнение 1-го порядка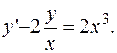 
Замена: 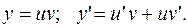Получаем: 
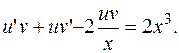
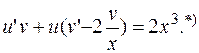
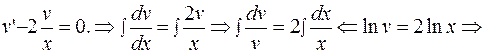
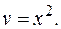
Подставляем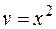 
в уравнение 
: 
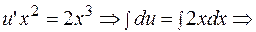
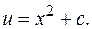Следовательно 
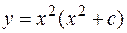- общее решение.
ПРИМЕР 2.11. Решить дифференциальное уравнение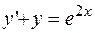 
.
РЕШЕНИЕ. Имеем линейное дифференциальное уравнение 1-го порядка. Выполняем замену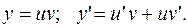
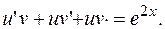
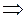
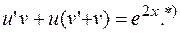
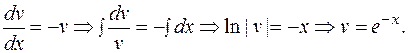Подставляем в и находим : 
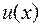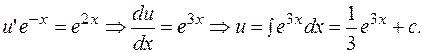
Общее решение исходного дифференциального уравнения:
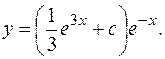
ПРИМЕР 2.12.
Решить дифференциальное уравнение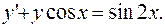 
.
РЕШЕНИЕ. Имеем линейное дифференциальное уравнение 1-го порядка. Выполняем замену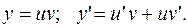
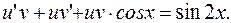
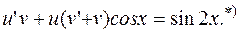
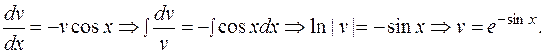
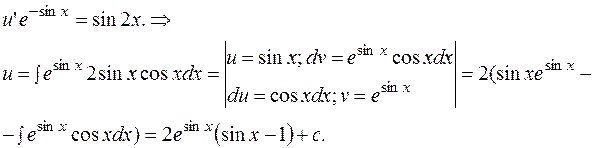
Окончательно: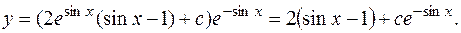 
2.2.7. Уравнения Бернулли. Уравнение Бернулли имеет вид :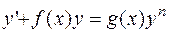 
, (2.14.)
где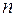 
- рациональное число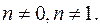 
Оно решается методом Бернулли, рассмотренным в 3.2.6.
ПРИМЕР 2.13. Решить дифференциальное уравнение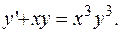 
РЕШЕНИЕ. Имеем уравнение Бернулли.
Выполняем замену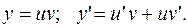
.
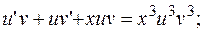
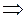
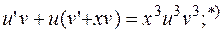
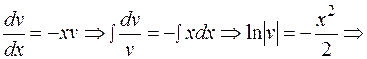
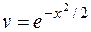Подставляем 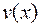в уравнение, помеченное знаком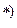
+ 
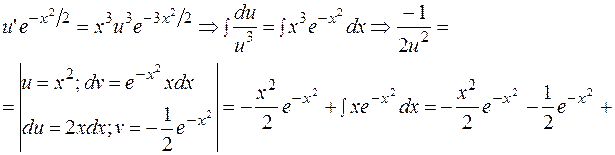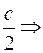
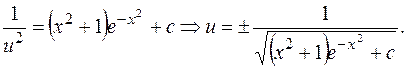
Таким образом,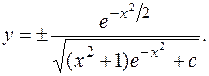 
Дата добавления: 2020-10-25; просмотров: 585;
Поиск по сайту
Узнать еще
- А. Уравнения движения точки в декартовых координатах
- Абсолютные и дифференциальные вихретоковые преобразователи
- Автономные системы, символические уравнения Вопрос 2
- Алгебраические и трансцендентные уравнения
- Алгоритм составления уравнения химической реакции
- Амплитудная характеристика усилителя. Нелинейные искажения
- Анализ качества эмпирического уравнения множественной
- Анализ уравнения Ленгмюра
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по географии
Публикации по медицине
