Экономические задачи, приводящие к дифференциальным уравнениям.

Основные понятия теории дифференциальных уравнений.

Часто, рассматривая какое-либо явление, не удается найти непосредственную зависимость переменных, но можно установить зависимость между этими переменными и их производными, выражающими, как известно, скорость изменения функции по аргументу.

Дифференциальным уравнением (ДУ) называется уравнение, связывающее искомую функцию одной или нескольких переменных и производные различных порядков данной функции.

Если искомая функция зависит от одного аргумента, то ДУ называется обыкновенным, если от нескольких, то - уравнением в частных производных.

В общем случае обыкновенное дифференциальное уравнение можно записать в виде:

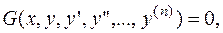(1.1)

где 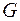- некоторая функция от 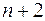переменных, 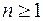, (то есть в составе уравнения имеется хотя бы одна производная).

Порядок старшей производной 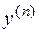определяет порядок дифференциального уравнения. Например,

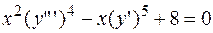- ДУ третьего порядка.

Дифференциальное уравнение п – го порядка называется разрешенным относительно старшей производной, если оно имеет вид:

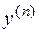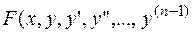= (1.2.)

Решением ДУ называется такая функция 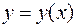, которая при подстановке её в исходное ДУ обращает его в тождество.

Например, из школьного курса физики известно, что уравнение гармонических колебаний 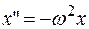имеет решения:

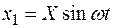и 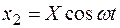.Взяв от этих решений вторые производные получаем исходное дифференциальное уравнение второго порядка:

.

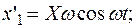
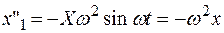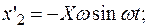
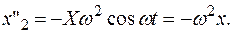
Задача о нахождении решения дифференциального уравнения сводится к задаче интегрирования данного ДУ.

График функции-решения ДУ называется интегральной кривой.

ПРИМЕР 1.1.Решить дифференциальное уравнение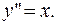

РЕШЕНИЕ. Поскольку 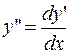, то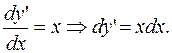

Проинтегрировав обе части уравнения, получаем:

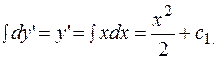
Преобразовываем полученное уравнение: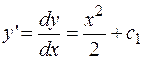

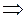
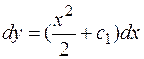и интегрируем ещё раз: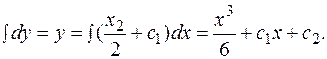

Видно, что решение исходного уравнения неоднозначно, так как величины 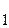с и с 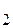могут принимать различные значения. Таким образом, дифференциальное уравнение задаёт семейство интегральных кривых. Произвольных постоянных с 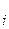в решении дифференциального уравнения появляется столько, сколько раз его приходится интегрировать. То есть порядок дифференциального уравнения определяет количество независимых переменных с 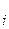. Такое решение дифференциального уравнения называется общим.

Для выделения однозначно определенной интегральной кривой (получения единственного решения) необходимо определить значения произвольных постоянных с 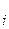. Для этого достаточно указать начальные условия, то есть значения зависимой переменной и n-1 её производных меньшего порядка при конкретном значении аргумента. Полученное решение называется частным.

ПРИМЕР 1. 2. Для дифференциального уравнения, данного в примере 1, найти частное решение при начальных условиях: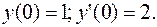

РЕШЕНИЕ.

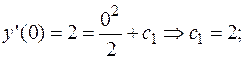
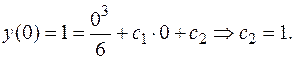
Следовательно, частное решение исходного дифференциального уравнения при заданных начальных условиях:

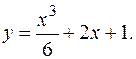
Таким образом, при решении дифференциального уравнения находят общее решение 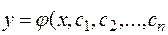), которое является функцией переменно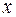й и 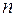произвольных независимых постоянных 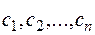. Если заданы начальные условия, то находят и частное решение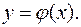

Задачу отыскания частного решения дифференциального уравнения по заданным начальным условиям называют задачей Коши.

Заметим, что;

если решение находят в неявном виде, то его называют общим или частным интегралом;

иногда решение удобней найти в виде .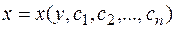

Роль произвольных независимых постоянных 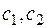можно определить, сравнив общее решение рассмотренного в примере 1 дифференциального уравнения второго порядка 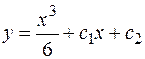с уравнением прямой 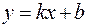. Угловой коэффициент 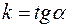характеризует наклон прямой к оси абсцисс, а величина 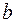- сдвиг прямой вдоль оси ординат. Очевидно, что постоянная с 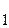характеризует поворот кривой относительно системы координат, а постоянная с 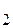характеризует сдвиг этой кривой вдоль оси ординат.

Так, если графиками задано семейство интегральных кривых дифференциального уравнения первого порядка и задано начальное условие 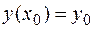, то та кривая, которая проходит через точку с координатами 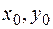и определяет частное решение заданного дифференциального уравнения.

Чтобы решить обратную задачу, то есть составить дифференциальное уравнение, которому удовлетворяют кривые заданного семейства 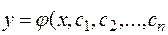) следует продифференцировать это общее решение 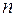раз, помня, что у –функция независимой переменной х, а затем из полученных равенств исключить постоянные .

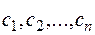ПРИМЕР 1.3. Составить дифференциальное уравнение второго порядка семейства кривых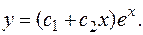

РЕШЕНИЕ. Берем производные:

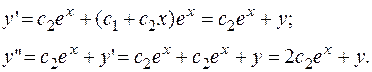
Находим 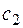из предпоследнего равенства: .

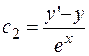Вставляем его в последнее равенство и исключаем 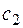из него:

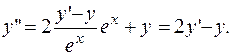
Таким образом, 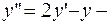искомое дифференциальное уравнение.

Экономические задачи, приводящие к дифференциальным уравнениям.

<12 3 4 5 6 7 >

Дата добавления: 2020-10-25; просмотров: 688;