Приклади визначення переміщень
Приклад 2.1.1 Для консольної балки, що навантажена силою 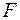 та розподільним навантаженням
та розподільним навантаженням 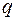 на ділянці довжиною
на ділянці довжиною 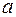 визначити вертикальне переміщення перерізу
визначити вертикальне переміщення перерізу 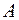 −
−  .
.
| Дано: 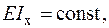 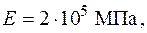 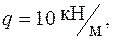 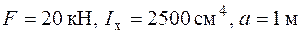 .
Визначаємо опорні реакції .
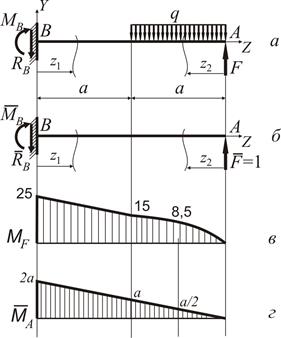
Визначаємо опорні реакції 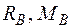 (рис. 2.6 а).
(рис. 2.6 а).
|
Рисунок 2.6
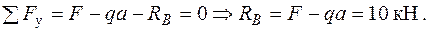
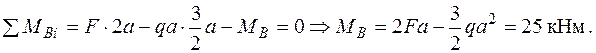
Навантажуємо балку одиничною силою у точці А (рис. 2.6 б), де треба визначити переміщення і визначаємо опорні реакції 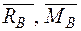 .
.
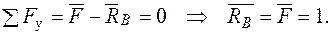
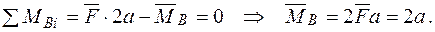
Записуємо рівняння згинальних моментів на ділянках балки від зовнішніх навантажень 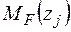 і одиничного навантаження
і одиничного навантаження 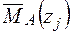 .
.
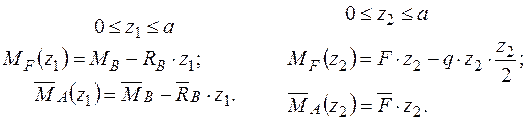
Визначаємо вертикальне переміщення перерізу 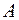 −
− 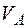 двома способами. По-перше, застосуємо інтеграл Максвелла – Мора:
двома способами. По-перше, застосуємо інтеграл Максвелла – Мора:
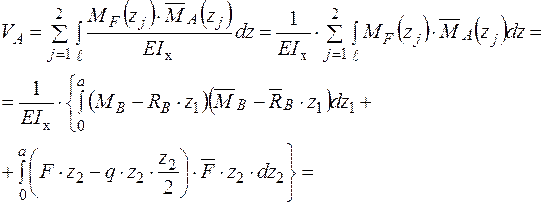
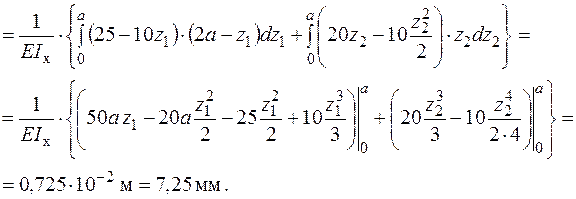
Додатне значення прогину 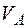 зазначає, що переріз
зазначає, що переріз 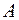 переміщується в напрямку дії одиничного зусилля
переміщується в напрямку дії одиничного зусилля 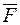 .
.
По-друге, для визначення прогину в перерізі А застосуємо графоаналітичний спосіб. Для цього необхідно мати епюри згинального моменту від зовнішнього 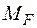 (рис. 2.6 в) та одиничного
(рис. 2.6 в) та одиничного 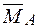 (рис. 2.6 г) навантажень. На ділянці, де
(рис. 2.6 г) навантажень. На ділянці, де 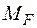 − квадратична парабола, необхідно використовувати правило Симпсона – Корноухова (2.6), а на ділянці з лінійною залежністю – правило трапецій (2.5):
− квадратична парабола, необхідно використовувати правило Симпсона – Корноухова (2.6), а на ділянці з лінійною залежністю – правило трапецій (2.5):
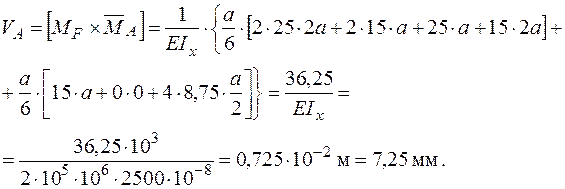
Двома методами отримано однакові результати, тому у наступних прикладах використовуємо графоаналітичний спосіб Верещагіна.
Приклад 2.1.2
| Для шарнірно обпертої балки, навантаженою згинальним моментом 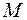 та силою та силою 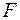 , визначити кутове переміщення в точці , визначити кутове переміщення в точці 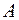 − − 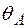 .
Дано: .
Дано: 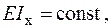
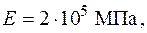
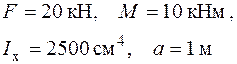 Визначаємо опорні реакції
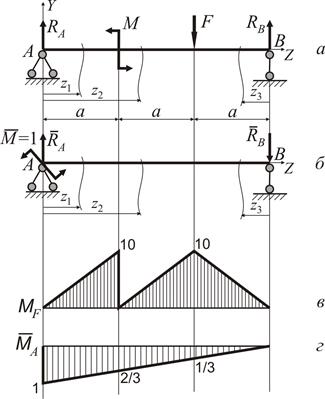
Визначаємо опорні реакції 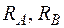 (рис. 2.7 а). (рис. 2.7 а).
|
Рисунок 2.7
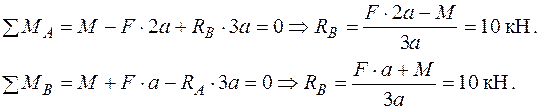
Навантажуємо балку одиничним моментом в перерізі А (рис. 2.7 б), де треба визначити кутове переміщення і визначаємо опорні реакції 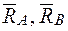 :
:
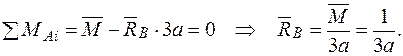
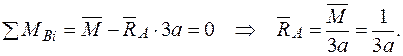
Записуємо рівняння згинальних моментів від зовнішніх навантажень 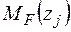 і одиничного навантаження
і одиничного навантаження 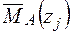 на ділянках балки та будуємо епюри (рис. 2.7 в,г).
на ділянках балки та будуємо епюри (рис. 2.7 в,г).
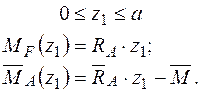
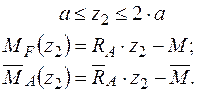
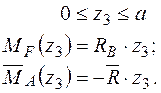
Визначаємо кут повороту графоаналітичним методом. На ділянках 2 та 3 використаємо правило Верещагіна, на ділянці 1 – правило трапецій:
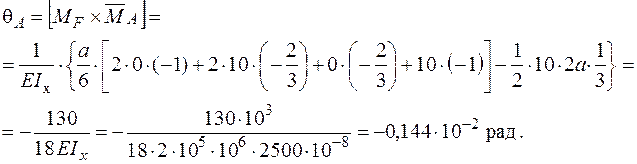
Негативне значення кута повороту 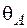 зазначає, що переріз А повертається в напрямку протилежному дії одиничного моменту
зазначає, що переріз А повертається в напрямку протилежному дії одиничного моменту 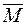 , тобто в напрямку обертання часової стрілки.
, тобто в напрямку обертання часової стрілки.
Приклад 2.1.3
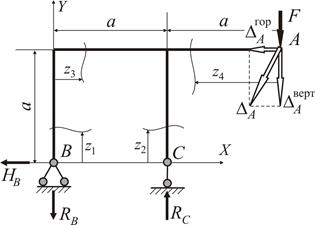
| Для рамної конструкції, шарнірно обпертої в точках 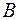 і і 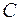 , визначити повне лінійне переміщення в точці , визначити повне лінійне переміщення в точці 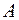 − − 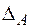 .
Дано: .
Дано: 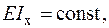
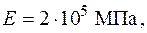
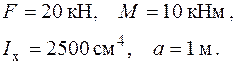
|
Рисунок 2.8
Визначаємо опорні реакції 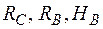 :
:
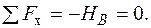
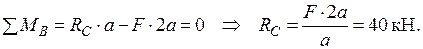
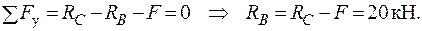
Визначення повного переміщення 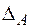 точки А складається з двох частин: знаходження вертикального
точки А складається з двох частин: знаходження вертикального 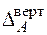 та горизонтального
та горизонтального 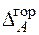 переміщень.
переміщень.
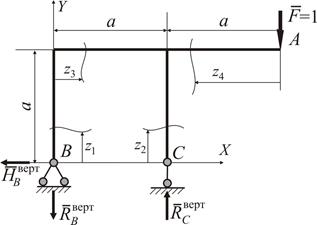
| Для визначення вертикального переміщення 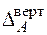 допоміжну систему (рис. 2.9) навантажуємо одиничною вертикальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції
допоміжну систему (рис. 2.9) навантажуємо одиничною вертикальною силою у точці А, де треба визначити це переміщення і визначаємо опорні реакції
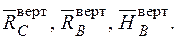
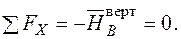
|
Рисунок 2.9
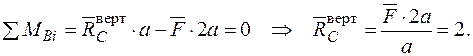
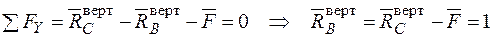 .
.
В більшості випадків при визначенні переміщень в балках та пласких рамах можна враховувати тільки вплив згинального моменту.
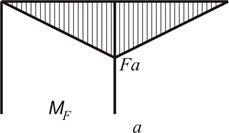
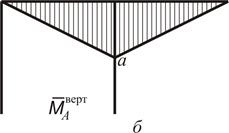
Записуємо рівняння згинальних моментів від зовнішніх навантажень 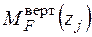 і одиничного навантаження
і одиничного навантаження 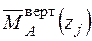 на ділянках рами та будуємо епюри (рис. 2.10 а,б):
на ділянках рами та будуємо епюри (рис. 2.10 а,б):
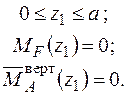
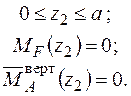
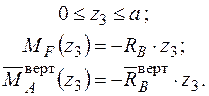
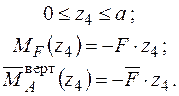
| 
|
Рисунок 2.10
Для визначення вертикального переміщення в перерізі А використаємо графоаналітичний метод Верещагіна:
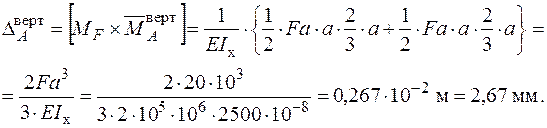
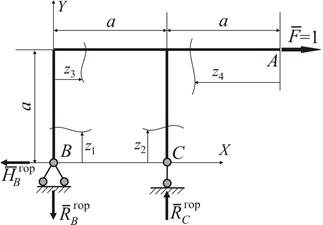
| Для визначення горизонтального переміщення 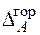 допоміжну систему навантажуємо одиничною горизонтальною силою у точці А, визначаємо опорні реакції (рис. 2.11) допоміжну систему навантажуємо одиничною горизонтальною силою у точці А, визначаємо опорні реакції (рис. 2.11) 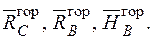
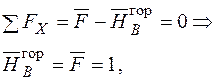
|
Рисунок 2.11

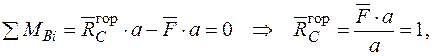
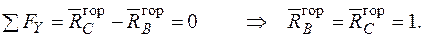
Записуємо рівняння згинальних моментів від зовнішніх навантажень 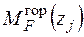 і одиничного навантаження
і одиничного навантаження 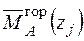 на ділянках рами:
на ділянках рами:
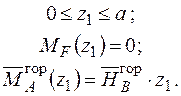
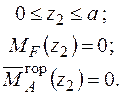
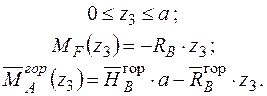
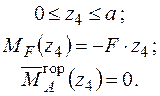
Будуємо відповідні епюри (рис. 2.12).
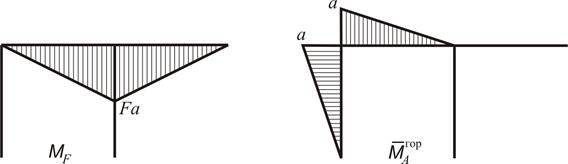
|
Рисунок 2.12
Визначаємо горизонтальне переміщення в перерізі 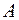 :
:
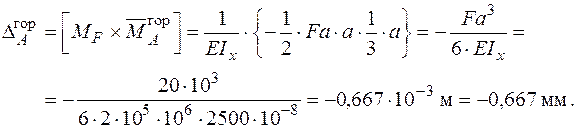
Вектор повного переміщення 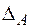 дорівнює векторній сумі вертикального
дорівнює векторній сумі вертикального 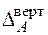 та горизонтального
та горизонтального 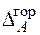 переміщень (рис. 2.8). Його числове значення визначається за формулою:
переміщень (рис. 2.8). Його числове значення визначається за формулою:
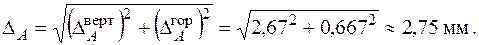
Дата добавления: 2020-10-14; просмотров: 1016;











