Аналітичне визначення головного вектора та головного моменту

Розглянемо детальніше поняття про момент сили відносно точки, скориставшись (2.33). Припустимо, що в точці N прикладена сила 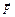. Знайдемо момент, утворений силою 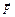відносно центра моментів О (рис.2.25):

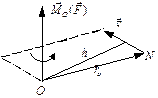
рис.2.25

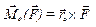,(а)

де 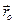- радіус-вектор, проведений з центру моментів О в точку прикладання сили .

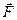Вектор 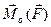напрямлений вздовж перпендикуляра до площини, утвореної векторами 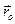та 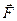в той бік, звідки обертання тіла, яке ніби виконує сила 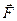, здається таким, що відбувається проти годинникової стрілки.

За величиною момент сили 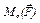дорівнює площі паралелограма, побудованого на сторонах 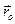та 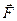. Перпендикуляр, опущений з центра моментів О на лінію дії сили 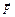, називається плечем сили та позначається буквою h. Момент сили дорівнює добутку сили на плече

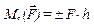. (2.36)

Момент сили додатній, якщо вона ніби намагається створити обертання навколо центра моментів проти руху годинникової стрілки. Якщо лінія дії сили перетинає центр моментів, то плече сили дорівнює нулю (h=0) і момент сили обертається в нуль.

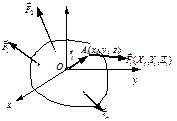
рис.2.26

Виведемо аналітичні формули, які визначають головний вектор та головний момент. Припустимо, задано тіло, до якого прикладена система сил 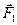, ,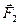..., . 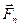Проведемо декартову систему координат з початком в точці О (рис.2.26). Припустимо, відомі координати точок прикладання x_i, y_i, z_i та проекції сил на осі координат X_i, Y_i, Z_i. Для аналітичного визначення вектора достатньо знати його проекції на осі координат, отримаємо

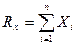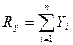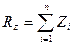; ; . (2.37)

З (2.37) видно, що проекції головного вектора на осі координат дорівнюють алгебраїчним сумам проекцій прикладених сил.

Проектуючи праву та ліву частини рівності (2.34) на осі координат, знайдемо проекції головного моменту на осі координат:

;

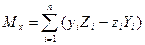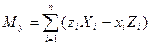; (2.38)

.

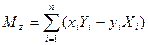Якщо відомі проекції вектора на осі координат, то вектор повністю визначений. Модуль головного вектора й головного моменту та їх напрямні косинуси можна визначити за формулами, відомими з аналітичної геометрії.