Обчислення інтеграла Мора способом перемноження епюр

Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр прямолінійна. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епюри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями.

Правило Верещагіна. Графоаналітичний спосіб визначення інтеграла Мора був запропонований О.М. Верещагіним. Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження повинна бути прямолінійною (рис. 2.3).

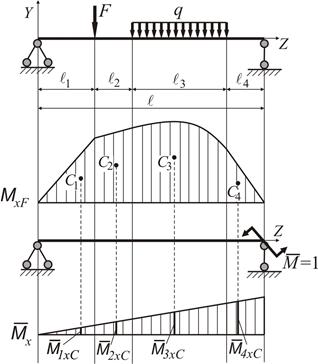
Рисунок 2.3

Згідно формули Верещагіна інтеграл Мора дорівнює добутку площі 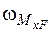епюри від зовнішнього навантаження 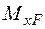на ординату одиничної епюри 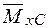, розташованої під центром ваги епюри від заданого зовнішнього навантаження [1]:

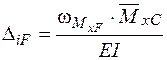(2.3)

Якщо обидві епюри прямолінійні, можна множити площу будь-якої з них на ординату іншої під центром ваги першої.

Коли епюра 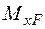має складний вигляд, то її слід розбити на прості фігури, для яких легко визначити площу і положення центра ваги. При цьому кожну з площин треба множити на ординату одиничної епюри під центром ваги відповідної площі. Ординати в цьому разі зручно позначати замість 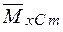літерами 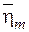, де 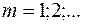− номер ділянки.

Отже,

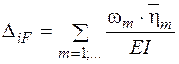(2.4)

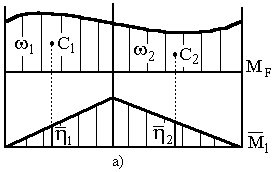
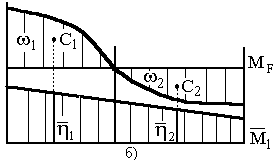
Користуючись способом Верещагіна, необхідно пам'ятати, що добуток епюр позитивний, якщо ординати обох епюр відкладені з одного боку від осі стержня рами, і негативний, якщо ординати епюр відкладені з різних сторін. В тих випадках, коли одна з епюр криволінійна, береться площа криволінійної епюри, а ордината під її центром ваги з прямолінійної епюри.Особливості застосування правила Верещагіна видно з рис. 2.4 а,б.

Рисунок 2.4

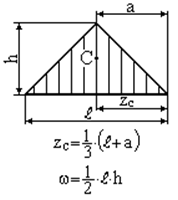
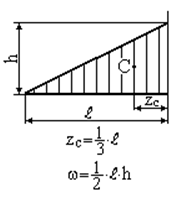
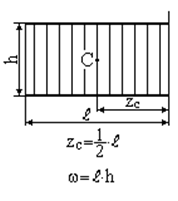
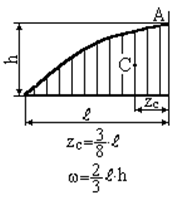
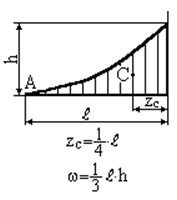
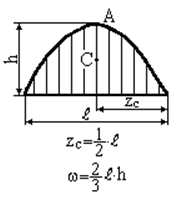
Зазначимо, що епюри внутрішніх силових факторів від зовнішнього та одиничного навантажень на окремих ділянках стержня складаються з досить простих фігур: прямокутник, трикутник, парабола і т.д. Площа 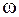та координата центра ваги 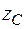цих простих фігур наведені в таблиці 2.1:

Таблиця 2.1 − Площі та координати центру ваги плоских фігур

Трикутник	Трикутник
Прямокутник	Парабола (квадратична) з вершиною в т. А
Парабола (квадратична) з вершиною в т.А	Парабола (квадратична) з вершиною в т.А

Наведемо ще два способу графоаналітичного визначення інтеграла Мора.

Правило трапецій (тільки для лінійних епюр – рис. 2.5 а).У випадку, коли епюра від зовнішніх навантажень 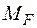, як і одинична 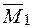є лінійною, формула Верещагіна (2.3) набуває вигляду

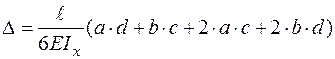. (2.5)

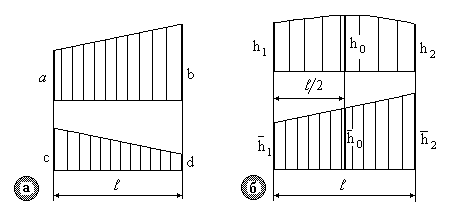
Рисунок 2.5

Правило Симпсона − Корноухова (для лінійних епюр та квадратичних парабол − рис. 2.5 б). Якщо одна з епюр є квадратичною параболою або прямою, а інша − прямою, то ефективним є застосування формули Симпсона − Корноухова:

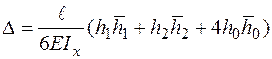. (2.6)

Тут 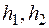− крайні ординати епюри 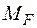(нелінійної або лінійної) на ділянці; - крайні ординати одиничної епюри (лінійної) на ділянц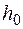і; і 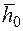− середні ординати епюр на ділянці.