Порядок виконання завдання
1. Виписати для заданого варіанту числові дані. В певному масштабі накреслити схему заданої системи з зазначенням її лінійних розмірів і зовнішніх навантажень.
2. Встановити ступінь статичної невизначуваності системи.
3. Розглянути можливі варіанти основної системи і вибрати з них раціональний для проведення подальших розрахунків.
4. Зобразити еквівалентну схему.
5. Скласти систему канонічних рівнянь методу сил для даного варіанту основної системи.
6. Побудувати для вибраної основної системи епюри моментів від заданих навантажень та одиничних сил.
7. Обчислити коефіцієнти канонічних рівнянь методу сил.
8. Вирішити систему канонічних рівнянь і визначити невідомі зусилля 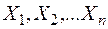 .
.
9. Побудувати остаточні епюри внутрішніх силових факторів для заданої статично невизначуваноїсистеми.
10. З умови міцності провести розрахунок розмірів круглого або квадратного перерізу.
РПЗ складається з двох обов’язкових для рішення задач:
1. Розкрити статичну невизначуваність багатопрольотної нерозрізної балки (додаток 2.1), побудувати епюри згинального моменту та поперечної сили, визначити розміри перерізу. Чисельні дані наведені в таблиці Д2.1.
2. Розкрити статичну невизначуваність плоскої рами (додаток 2.2), побудувати епюри згинального моменту, поперечної та поздовжньої сил. Визначити розміри перерізу. Чисельні дані наведені в таблиці Д2.2.
2.3.2 Зразок виконання задачі 1 − Розрахунок статично невизначуваної балки
Дано:
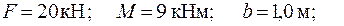
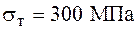 ;
; 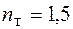 .
.
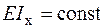 .
.
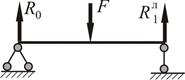
Необхідно: Для статично невизначуваної балки (рис. 2.25) побудувати епюри згинального моменту і поперечної сили, визначити розміри квадратного перерізу.
− Визначаємо ступень статичної невизначуваності системи (рис. 2.25 а): 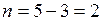 .
.
− Обираємо основну систему (рис. 2.25 б) і будуємо еквівалентну систему (рис. 2.25 в).
− Прикладаємо до основної системи тільки зовнішнє навантаження (рис. 2.25 г) і будуємо «вантажну» епюру 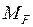 (рис.2.25 д):
(рис.2.25 д):
Ділянка 0-1
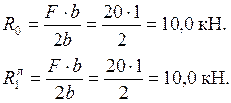
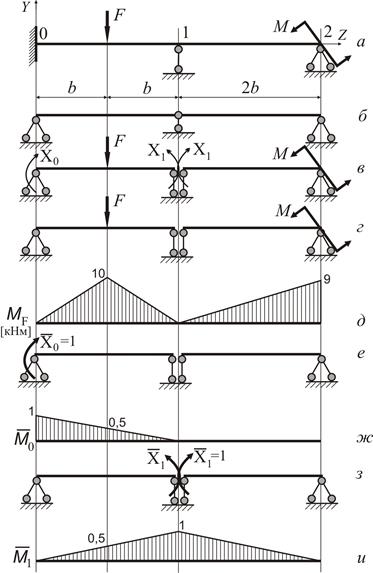
|
Ділянка 1-2

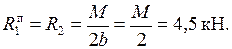 − Прикладаємо одиничний момент
− Прикладаємо одиничний момент 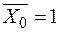 та будуємо одиничну епюру та будуємо одиничну епюру 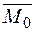 (рис. 2 25 е, ж).У тієї ж послідовності будуємо епюру (рис. 2 25 е, ж).У тієї ж послідовності будуємо епюру 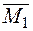 (рис. 2.25. з, и).
− Записуємо канонічні рівняння методу сил: (рис. 2.25. з, и).
− Записуємо канонічні рівняння методу сил:
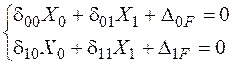 .
− Визначаємо коефіцієнти: .
− Визначаємо коефіцієнти:
|
Рисунок 2.25
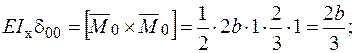
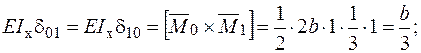
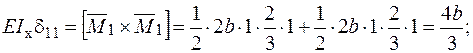
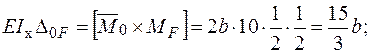
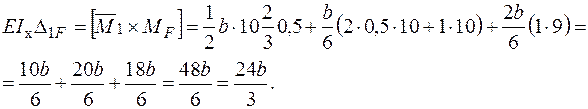
− Вирішуємо систему рівнянь:
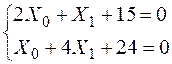 ;
; 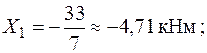
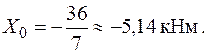
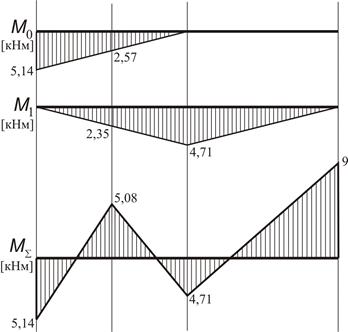
| − Будуємо епюри від опорних моментів:
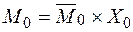
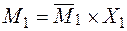 .
− Будуємо епюру сумарних згинаючих моментів: .
− Будуємо епюру сумарних згинаючих моментів:
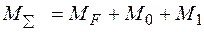
|
Деформаційна перевірка №1:
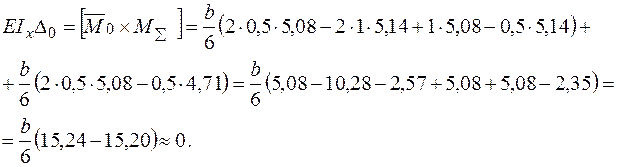 Відносна похибка складає:
Відносна похибка складає:
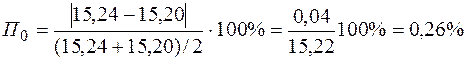 .
.
Деформаційна перевірка №2:
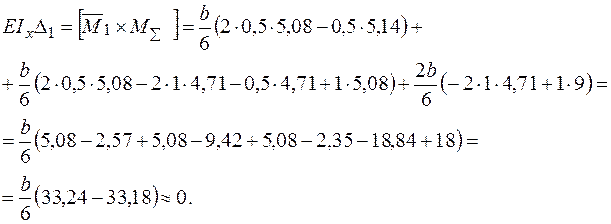 Відносна похибка складає:
Відносна похибка складає:
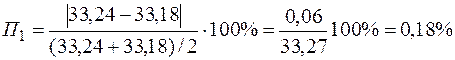 .
.
З умови міцності визначаємо розмір квадратного перерізу: 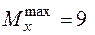 кНм;
кНм; 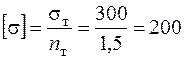 МПа .
МПа .
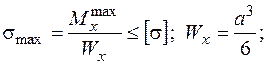 звідки
звідки 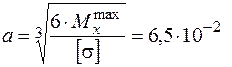 м.
м.
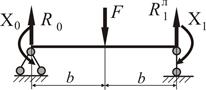
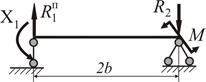
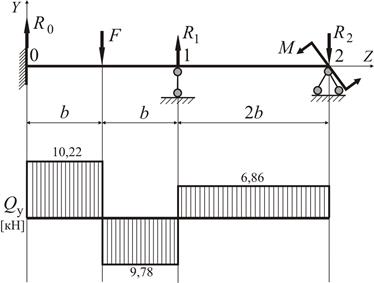
Будуємо епюру поперечних сил 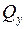 (рис.2.26). Для цього знаходимо реакції опор:
(рис.2.26). Для цього знаходимо реакції опор:
| 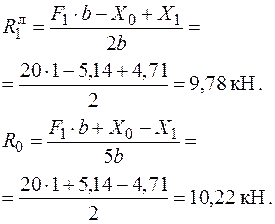
|
| 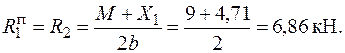
|
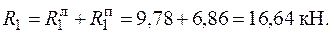
|
Рисунок 2.26
2.3.3 Зразок виконання задачі 2 − Розрахунок статично невизначуваної рами
Дано: 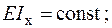
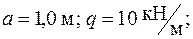
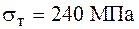 ;
; 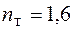 .
.
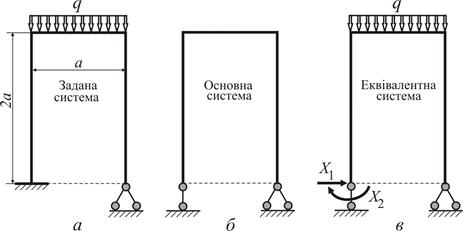
Необхідно:Розкрити статичну невизначуваність рами (рис.2.27 а), побудувати епюру згинального моменту та визначити з умови міцності діаметр круглого перерізу.
− Встановимо ступінь статичної невизначуваності системи:
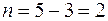 .
.
− Обираємо основну систему та відповідно до неї будуємо еквівалентну систему (рис. 2.27 б, в).
|
Рисунок 2.27
− Будуємо епюри:
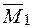 – рис. 2.28 а,
– рис. 2.28 а, 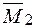 – рис. 2.28 б,
– рис. 2.28 б, 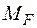 – рис. 2.28 в.
– рис. 2.28 в.
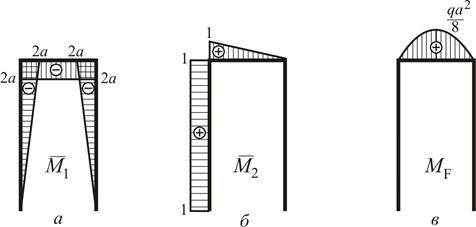
|
Рисунок 2.28
− Канонічні рівняння методу сил мають вигляд:
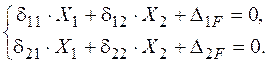
− Визначаємо коефіцієнти цієї системи:
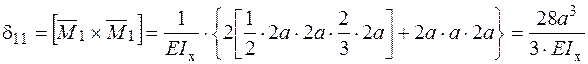 ;
;
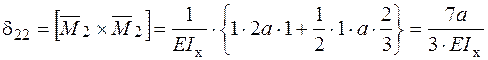 ;
;
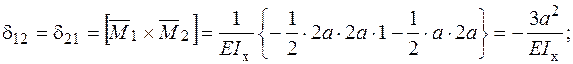
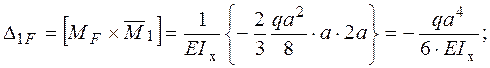
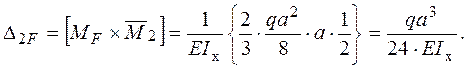
− Розв’язуємо систему канонічних рівнянь та визначаємо 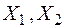 :
:
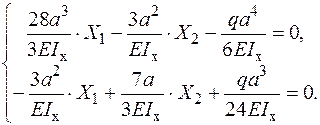
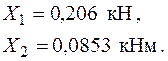
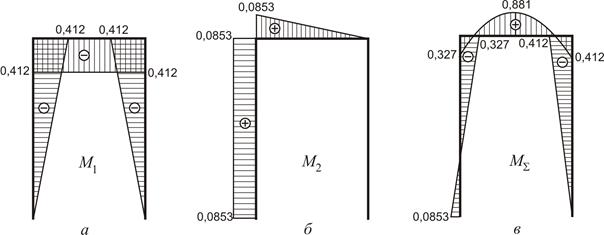
− Будуємо епюри згинальних моментів 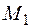 − рис. 2.29 а,
− рис. 2.29 а, 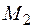 – рис. 2.29 б та сумарну епюру згинальних моментів
– рис. 2.29 б та сумарну епюру згинальних моментів 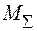 (рис. 2.29 в):
(рис. 2.29 в):
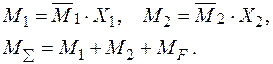
|
Рисунок 2.29
− Проводимо деформаційну перевірку:
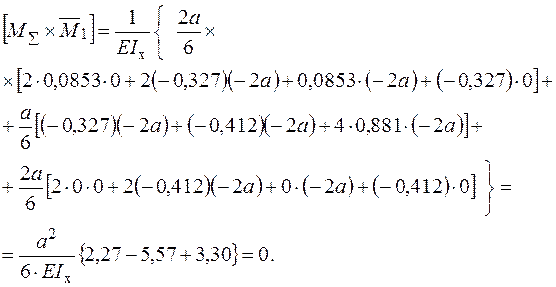
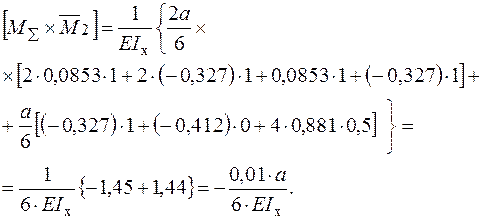
− Визначаємо відносну похибку:
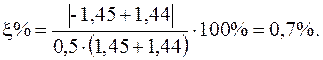
Висновок: задача розкриття статичної невизначуваності рами, та побудови епюри згинального моменту вирішена вірно в рамках допустимої похибки (<3%).
З умови міцності визначаємо діаметр круглого перерізу:
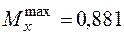 кНм;
кНм; 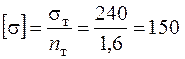 МПа.
МПа.
Нехтуємо впливом повздовжньої сили, тоді
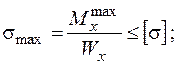
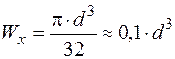 .
.
Звідки 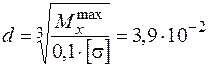 м.
м.
Дата добавления: 2020-10-14; просмотров: 683;











