Інтеграл Максвелла – Мора

Розглянемо балку довжиною 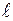, навантажену в точці 1 силою 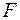(рис. 2.1). Визначимо переміщення 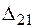(у точці 2 від сили, прикладеної в точці 1).

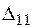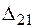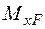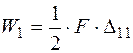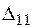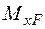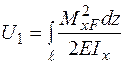1. Перший стан. У точці 1 прикладемо зосереджену силу F. Прогин у точці 1 дорівнює , у точці 2 − . У перерізах балки виникає згинальний момент від зовнішнього навантаження . Сила F прикладається статично і виконує роботу на шляху (див. графік на рис. 2.1.1). Визначаємо потенціальну енергію деформації, що виражена через згинальний момент [1]: . Потенціальна енергія деформації 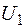чисельно дорівнює роботі зовнішніх сил 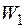, тобто: .

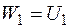2. Другий стан. У точці 2 статично прикладемо одиничну силу, що, згинаючи балку, виконує роботу (див. графік на рис. 2.1.2) на переміщенні 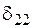. У перерізах балки виникає згинальний момент 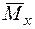від одиничної сили. Робота одиничної сили 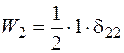. Потенціальна енергія деформації 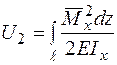. Як і в попередньому випадку .

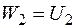3. Третій стан. У точці 2 статично прикладемо одиничну силу, що, деформуючи балку, виконує роботу 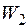на переміщенні 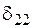(див. графік на рис. 2.1.3). До деформованої балки статично у точці 1 прикладемо зосереджену силу 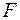, що, деформуючи балку з уже прикладеною одиничною силою, виконує роботу 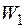(див. графік) на переміщенні 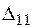. Точка 2 одержить ще переміщення 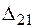, а одинична сила виконає роботу 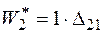(див. графік) на переміщенні 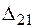. Від дії сили 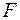й одиничного навантаження в перерізах балки виникає сумарний згинальний момент .

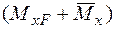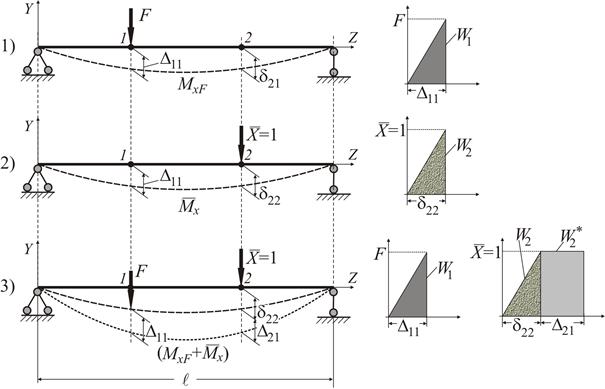
Рисунок 2.1

Робота двох сил визначиться як:

,

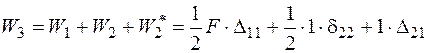а потенціальна енергія пружної деформації виразиться через сумарний згинальний момент як:

.

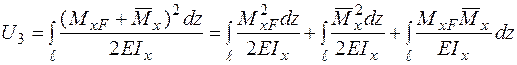Порівнюючи вирази для 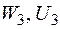, після нескладних перетворень одержимо вираз для визначення переміщень, що носить назву «інтеграл Мора»:

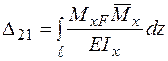. (2.1)

Якщо узагальнити вираз (2.1) на випадок сумісної дії згинання, розтягання та кручення, отримаємо формулу Максвелла − Мора [2]:

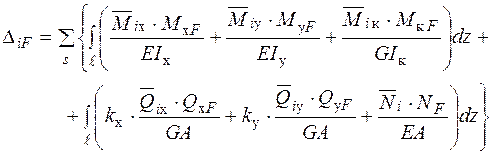. (2.2)

Індекси “x”, “y” в формулі (2.1.2) позначають головні осі перерізу ділянки стержня, індекс “к” – крутний момент, s − номер ділянки довжиною 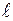, 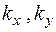− коефіцієнти, що залежать від форми перерізу.

Порядок визначення переміщень за допомогою інтеграла

Максвелла − Мора

1. Прикладаємо зовнішнє навантаження, визначаємо опорні реакції, розбиваємо балку на ділянки, записуємо вирази (функції) згинального моменту 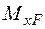для кожної ділянки.

2. Замість заданого зовнішнього навантаження у точці, переміщення якої визначаємо, прикладаємо:

а) одиничну силу (при визначенні прогину);

б) одиничний момент (при визначенні кута повороту перерізу).

Визначаємо опорні реакції, на кожній ділянці записуємо вирази (функції) згинального моменту .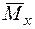

3. Підставляємо функції (вирази) 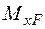і 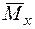в інтеграл Мора (2.1) та робимо відповідні обчислення.

4. Якщо результат обчислень є додатним, то напрямок переміщення збігається з напрямком одиничного навантаження і навпаки.

Приклад

Консольна балка постійного поперечного перерізу (EI_x=const) довжиною 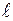навантажена на кінці зосередженою силою 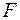(рис. 2.2 а). Визначити прогин 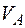та кут 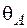повороту на кінці консолі.

1. Запишемо функцію 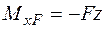(рис. 2.2 а).

2. У точці 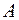прикладаємо одиничну силу (рис. 2.2 б) та записуємо функцію .

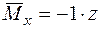3. Підставляюч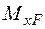и й 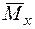в інтеграл Мора (2.1), одержимо: .

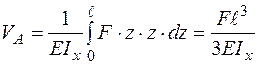4. Для визначення кутового переміщення у точці 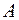прикладаємо одиничний момент (рис. 2.2 в) та записуємо функцію .

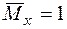5. Підставляючи 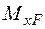та 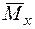в інтеграл Мора, одержимо: .

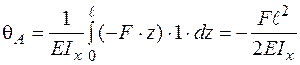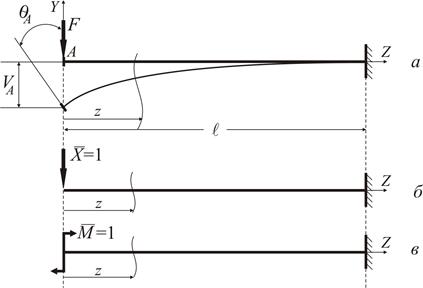
Рисунок 2.2

Результат обчислення прогину 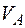додатний, тому напрямок дійсного переміщення збігається з напрямком одиничної сили. Результат обчислення кута повороту 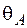негативний, тому дійсний напрямок повороту перерізу в точці 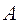є протилежним напрямку одиничного моменту.