Перевірка правильності розрахунків
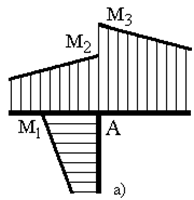
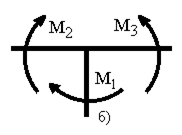
Після визначення невідомих зусиль з канонічних рівнянь методу сил та побудови епюри моментів 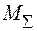 для заданої системи, слід зробити перевірку. Спочатку необхідно з'ясувати виконання умов статичної рівноваги вузлів рами, для цього необхідно вирізати кожний вузол і дію відкинутих частин замінити моментами. Величину моментів взяти з епюри
для заданої системи, слід зробити перевірку. Спочатку необхідно з'ясувати виконання умов статичної рівноваги вузлів рами, для цього необхідно вирізати кожний вузол і дію відкинутих частин замінити моментами. Величину моментів взяти з епюри 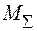 . При цьому стрілки, що вказують дію згинаючого моменту, направлені у бік стислих волокон (рис. 2.18 а,б).
. При цьому стрілки, що вказують дію згинаючого моменту, направлені у бік стислих волокон (рис. 2.18 а,б).
|
|
Рисунок 2.18
Алгебраїчна сума моментів повинна дорівнювати нулю:
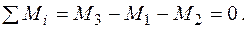
Перевірка правильності побудованих епюр згинальних моментів (перевірка виконання умови еквівалентності) також проводиться шляхом визначення переміщення в місцях прикладення зайвих невідомих зусиль(деформаційна перевірка). Для цього необхідно перемножити епюру згинальних моментів 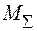 і епюри згинальних моментів
і епюри згинальних моментів 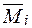 від одиничних навантажень:
від одиничних навантажень: 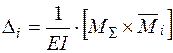 .
.
Якщо ці переміщення з заданою точністю (3¸5%) будуть дорівнювати нулю, то епюра 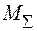 побудована вірно.
побудована вірно.
Приклади розкриття статичної невизначуваності
Приклад 2.2.1
Дано: 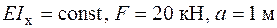 .
.
Визначити: Для шарнірно обпертої балки, навантаженої силою F, побудувати епюри згинального моменту і поперечної сили.
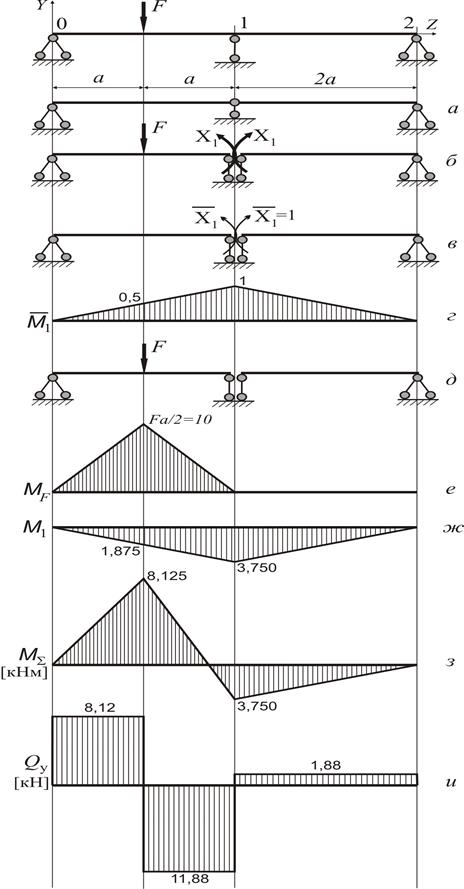
− знаходимо ступінь статичної невизначуваності балки (рис. 2.19 а): 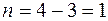 .
.
− обираємо основну систему (рис. 2.19 б). Для цього встановимо додатковий шарнір в тіло балки над проміжною (середньою) опорою. При цьому згинальний момент в даному перерізі перетворюється на нуль. Тоді балку можна уявити складеною з двох незалежних балок (рис. 2.19 в).
− будуємо еквівалентну систему шляхом прикладання зовнішньої сили 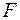 і невідомого згинального моменту
і невідомого згинального моменту 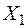 в перерізі з одиночним шарніром (рис. 2.19 в).
в перерізі з одиночним шарніром (рис. 2.19 в).
− до основної системи прикладаємо одиничний момент 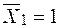 (рис. 2.19 г) і будуємо епюру
(рис. 2.19 г) і будуємо епюру 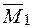 (рис. 2.19 д).
(рис. 2.19 д).
− до основної системи прикладаємо зовнішнє навантаження (силу 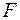 ) (рис. 2.19 е) і будуємо «вантажну» епюру
) (рис. 2.19 е) і будуємо «вантажну» епюру 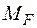 (рис. 2.19 ж).
(рис. 2.19 ж).
− записуємо канонічне рівняння метода сил: 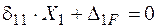 . Тут
. Тут 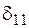 – взаємний кут повороту в місці встановлення додаткового шарніра від прикладання одиничного згинального моменту в напрямку його дії, а
– взаємний кут повороту в місці встановлення додаткового шарніра від прикладання одиничного згинального моменту в напрямку його дії, а 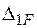 – взаємний кут повороту в місці встановлення одиничного шарніра від прикладання зовнішнього навантаження (сили
– взаємний кут повороту в місці встановлення одиничного шарніра від прикладання зовнішнього навантаження (сили 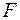 ).
).
− визначаємо коефіцієнти канонічного рівняння метода сил:
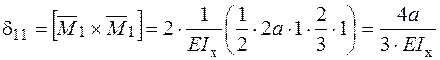 ,
,
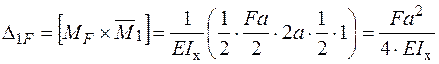 .
.
− розв’язуємо канонічне рівняння і визначаємо 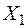 :
:
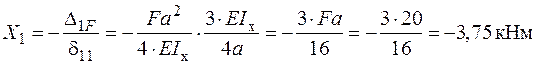
та будуємо епюру  від знайденого моменту
від знайденого моменту  (рис. 2.19 з).
(рис. 2.19 з).
|
Рисунок 2.19
− шляхом складання по ділянках балки епюри 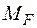 і епюри
і епюри 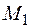 будуємо епюру
будуємо епюру 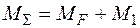 (рис. 2.19 и).
(рис. 2.19 и).
− проводимо деформаційну перевірку шляхом визначення взаємного кута повороту в місці одиночного шарніра. Якщо цей взаємний кут повороту з заданою точністю (3¸5%) буде дорівнювати нулю, то розрахунки по розкриттю статичної невизначуваності та побудови епюри 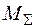 вірні. Для цього необхідно перемножити епюру згинальних моментів
вірні. Для цього необхідно перемножити епюру згинальних моментів 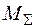 для статично невизначуваної системи і епюру згинальних моментів
для статично невизначуваної системи і епюру згинальних моментів 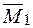 :
:
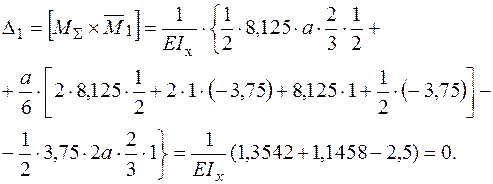
Епюра поперечних сил 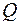 (рис. 2.19 к) будується з урахуванням опорних реакцій, які визначаються для еквівалентної системи (рис. 2.19 в) після знаходження моменту
(рис. 2.19 к) будується з урахуванням опорних реакцій, які визначаються для еквівалентної системи (рис. 2.19 в) після знаходження моменту 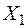 .
.
| Для ділянки балки 0-1:
|
| Для ділянки балки 1-2:
|
При цьому, для ділянок балки 0-1 та 1-2 опорні реакції знаходяться окремо, а сумарна реакція у першому шарнірі визначається за алгебраїчною сумою лівої і правої частки цієї реакції:
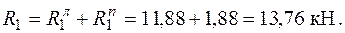
Приклад 2.2.2
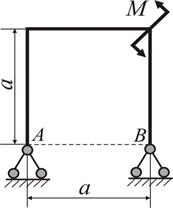 Рисунок 2.20
Рисунок 2.20
| Дано:
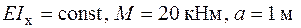 .
Визначити: Для прямокутної рами (рис. 2.20), навантаженої моментом М, побудувати епюри згинального моменту, поздовжніх та поперечних сил.
− Визначаємо ступінь статичної невизначуваності рами (рис. 2.20): .
Визначити: Для прямокутної рами (рис. 2.20), навантаженої моментом М, побудувати епюри згинального моменту, поздовжніх та поперечних сил.
− Визначаємо ступінь статичної невизначуваності рами (рис. 2.20): 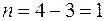 .
− Обираємо основну статично визначу- .
− Обираємо основну статично визначу-
|
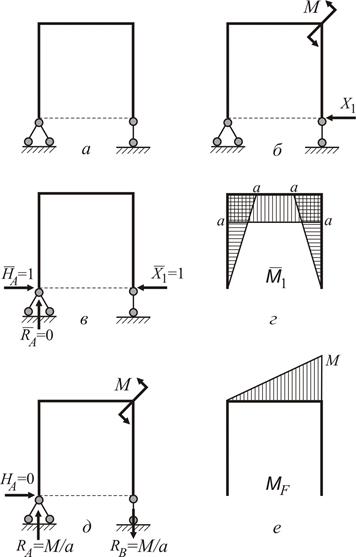
| вану систему (рис. 2.21 а). Для цього встановимо рухомий шарнір замість нерухомого в точці В.
− Будуємо еквівалентну систему шляхом прикладання зовнішнього моменту М і невідомої сили 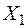 у точці В у напрямку відкинутого зв’язку (рис. 2.21 б).
− Будуємо епюру у точці В у напрямку відкинутого зв’язку (рис. 2.21 б).
− Будуємо епюру 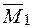 , для цього до основної системи прикладаємо одиничну силу , для цього до основної системи прикладаємо одиничну силу 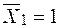 (рис. 2.21 в, г) .
− Будуємо епюру (рис. 2.21 в, г) .
− Будуємо епюру 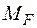 , для цього до основної системи прикладаємо зовнішнє навантаження (момент М) (рис. 2.21 д, е).
− Записуємо канонічне рівняння метода сил: , для цього до основної системи прикладаємо зовнішнє навантаження (момент М) (рис. 2.21 д, е).
− Записуємо канонічне рівняння метода сил:
|
Рисунок 2.21
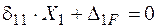 ,
,
тут 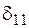 – лінійне переміщення у точці В у напрямку сили
– лінійне переміщення у точці В у напрямку сили 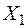 від одиничної сили
від одиничної сили 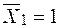 , а
, а 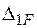 – лінійне переміщення у точці В у напрямку сили
– лінійне переміщення у точці В у напрямку сили 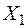 від прикладання зовнішнього навантаження (моменту М).
від прикладання зовнішнього навантаження (моменту М).
− Визначаємо коефіцієнти канонічного рівняння метода сил:
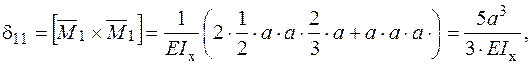
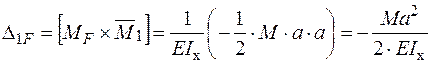 .
.
− Розв’язуємо канонічне рівняння і визначаємо 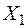 :
:
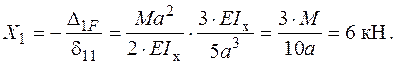
 аб
аб
|
Рисунок 2.22
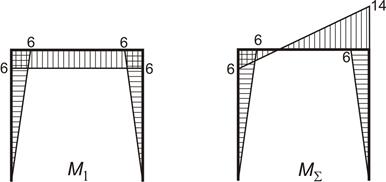
− Будуємо епюру 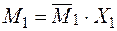 від знайденої сили
від знайденої сили 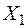 (рис. 2.22 а).
(рис. 2.22 а).
− Шляхом складання по ділянках балки епюри 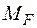 (рис. 2.21 е) і епюри
(рис. 2.21 е) і епюри 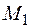 (рис. 2.22 а) будуємо епюру
(рис. 2.22 а) будуємо епюру 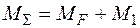 (рис. 2.22 б).
(рис. 2.22 б).
− Виконуємо деформаційну перевірку шляхом визначення лінійного переміщення 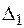 в напрямку
в напрямку 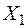 , яке з заданою точністю (
, яке з заданою точністю ( 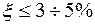 ) повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів
) повинно дорівнювати нулю. Для цього необхідно перемножити епюру згинальних моментів 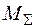 (рис. 2.22 б) і епюру згинальних моментів
(рис. 2.22 б) і епюру згинальних моментів 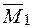 (рис. 2.21 г) г) :
(рис. 2.21 г) г) :
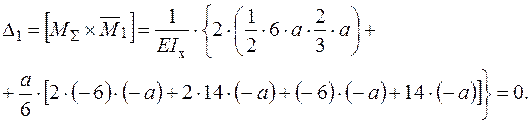
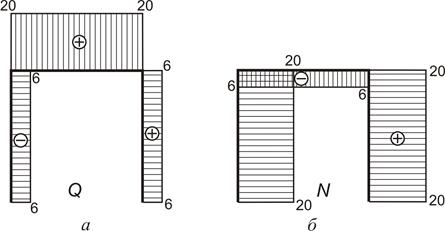
Епюри поздовжніх – 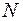 та поперечних –
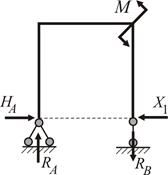
та поперечних – 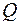 сил (рис. 2.24 а, б) будуються з урахуванням опорних реакцій в шарнірах А і В , які визначаються для еквівалентної системи (рис. 2.23) після знаходження сили
сил (рис. 2.24 а, б) будуються з урахуванням опорних реакцій в шарнірах А і В , які визначаються для еквівалентної системи (рис. 2.23) після знаходження сили 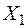 .
.
| 
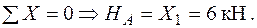
|
Рисунок 2.23
|
Рисунок 2.24
Дата добавления: 2020-10-14; просмотров: 737;











