Общий случай обратных связей.

Mатематическое определение обратных связей.

Дана функция:

y = F(x)

Введем в нее обратную связь:

y = F(x , y) = F(u) (5.3.2.,01)

В таком случае F(u) - неявная функция.

Это математическое определение функций с обратными связями.

Рассмотрим общий случай обратных связей.

Доказательство эквивалентности системы с ООС как системы с переходом процессов.

Рассмотрим отрицательную обратную связь. Выразим её как 2 функции (2 процесса).

Здесь первоначально рассматривается не процессовый переход, а процессы обратной связи, но в дальнейшем, мы сможем обнаружить два процесса процессового перехода – в выражении (5.3.2.,10).

x - аргумент сигнала ( или аргумент прямой связи )

x₀ – аргумент сигнала обратной связи ( или аргумент обратной связи )

у = F(x) = А – является функцией 1-го процесса. (5.3.2.,02)

у = F(x) = А – является внутренней функцией. ( см. главу 3.3. )

Функция у = F(x) = А – это функция прямой передачи.

у = F(x₀) = B – является функцией 2-го процесса. (5.3.2.,03)

у = F(x₀) = B – является внутренней функцией. ( см. главу 5.2.3. )

Функция у = F(x₀) = B – это функция прямой передачи с аргументом обратной связи.

По сути x и x₀ – это аргументы, но принадлежащие 2-м разным процессам. Для симметрии вводим y₀ –это результирующее значение функции при воздействии на неё обратной связи. При решении задачи об ООС, как раз вычисляется y₀.

Уравнение обратной связи выражается так:

y = F(x - x₀) (5.3.2.,04)

Функция F(x) является функцией 1-го процесса, а также является и внешней функцией (см. главу 5.2.3.)

Выразим функцию обратной связи. Представим её как сложную функцию, по отношению к у = F(x). Функция обратной связи будет выглядеть так:

у = H( F(x₀) ) (5.3.2.,05)

Начальные условия заданы. Теперь вычислим ООС.

Вычисляем x₀ :

у = H( F(x₀) ) (5.3.2.,05)

_

F(x₀) = H(y)

_ _

x₀ = F ( H ( y ) )

Из ( 4.05 ) находим уравнение для ООС:

_ _

y = F( x - F ( H ( y ) ) (5.3.2.,06)

Решение для уравнения ООС сводиться к нахождению x:

_ _

y = F( x - F ( H ( y ) )

_ _ _

F(y) = x - F ( H ( y ) ) (5.3.2.,07)

_ _ _

x = F(y) + F ( H ( y ) ) (5.3.2.,08)

Затем из условия у = F(x), получаем результирующее значение как y₀.

_ _ _

y₀.= F(x) = F( F(y) + F( H (y) ) ) (5.3.2.,09)

Функция прямой передачи: у = F(x)

и функция обратной передачи: у = F(x₀)

взаимно обратимы.

Это означает, что блок-схему обратной связи можно построить так, как изображено на рис. 5.12.:

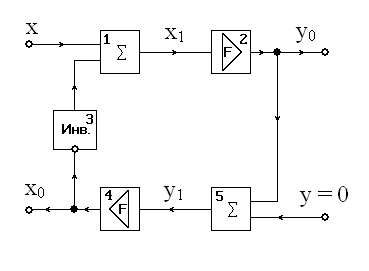
Рис. 5.12. Блок-схема системы с обратной связью. Внутри системы можно обнаружить процессовый переход. При этом одна из функций ( блок 2) будет внешней.

На рисунке 5.12.: блоки 1 и 5 - сумматоры; блоки 2 и 4 – функциональные усилители; блок 2 определяет функцию

y = F(x); б лок 4 определяет функцию

_ _

x₀ = F ( H ( y ) );

Блок 3 – аналоговый инвертор;

x₁ и y₁ - промежуточные значения сигналов:

_ _ _

x₁ = F(y) + F ( H ( y ) ) (5.3.2.,08)

у₁ = H( F(x₀) ) (5.3.2.,05).

От системы с обратной связью можно перейти к функции, которая моделирует переход от одного процесса к другому.

Функции, моделирующие переход между двумя процессами рассматриваются в главе 5.2.3. Это выражение выглядит так:

_

y ∙ (H(y))

y _рез = ---------------------- (5.3.2.,10)

_ _ _

F( F(y) +F(H(y)))

или:

F(x) ∙ F(x₀)

y _рез = ----------------- (5.3.2.,11)

y₀

Можно сравнить выражение (5.3.2.,10) с уравнением «весов»:

y = A = F1(x)

y = B = F2 (x)

__

y_рез = A ∙B / F ( F( A) + F( B) ) (5.2.3.,02)