Внешняя степенная функция процессового перехода по принципу результирующей максимизации.

Уравнение «весов», которое соответствует принципу результирующей максимизации, существует и записывается так:

y = A = F1(x)

y = B = F2 (x)

_N _______________

y_рез = A∙B ∙ √ A^-N + B^-N (5.2.6.,01)

Уравнение (5.2.6.,01) получается из (5.2.4.,01) путём замены показателя степени N на -N. То есть функция F, применённая в знаменателе является убывающей.

Уравнение такого типа создаёт переход от процесса к процессу , по принципу приближения к максимуму от этих двух процессов.

Приведём примеры объединения двух процессов по принципу приближения к максимуму от этих двух процессов.

На рисунке 5.7. построим процессовый переход по уравнению «весов» на основе степенной функции с показателем степени N=3 между функциями:

y = x² и y = 0,2 ∙ x + 50 .

Процессовый переход будет определяться следующей системой уравнений:

y = A = F1(x) = x²

y = B = F2 (x) = 0,2 ∙ x + 50

_N ___________

y_рез = A∙B ∙ √ A^-N + B^-N

N = 3

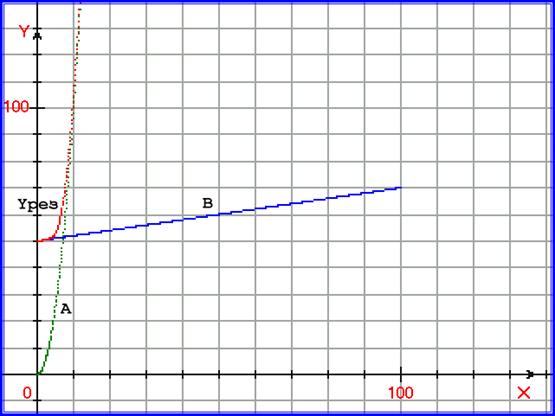
Рис. 5.7. График, иллюстрирующий одномерный процессовый переход. На графике построены функция y=A = x², функция y = B= 0,2∙x+50, а также функция y_рез =A∙B∙(A ^-N+B^-N) ^1/N , при N =3.

Задача о мини-максимизации и макси-минимизации.

На рисунке 5.8. показаны 4 области, образуемые пересечениями функций A и B.

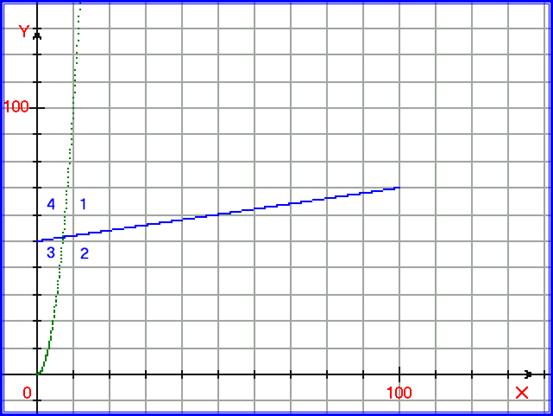
Рис. 5.8. области, образуемые пересечениями функций A и B.

Область 2 – это область для построения графика по принципу приближения к минимуму от двух процессов.

Область 4 – это область для построения графика по принципу приближения к максимуму от двух процессов.

Область 1 – это область макси-минимизации.

Область 3 – это область мини-максимизации.

Для областей 1 и 3 общего решения для поиска функции перехода из процесса в процесс пока не найдено.