Алгебра событий. Случайные события
1. Случайные события. В теории вероятностей окружающая нас жизнь изучается не во всей ее сложности, а только с одной определенной стороны. При этом строится некоторая схема (или модель), которая более или менее полно отражает интересующую нас сторону жизни. Например, в геометрии изучаются свойства фигур: точек, прямых, плоскостей и т. п. Но в реальной жизни мы не наблюдаем таких объектов — это результаты моделирования (схематизирования, абстрагирования) определенной стороны реальной жизни. В физике рассматриваются материальная точка, идеальный газ, абсолютно твердое тело и т. п. Это тоже модели определенной стороны реальной жизни — в природе мы не наблюдаем материальных точек, идеального газа, абсолютно твердого тела и т. п.
В теории вероятностей рассматривается следующая модель изучаемых явлений реальной жизни: проводится опыт (испытание), в результате которого происходят случайные события (обычно говорят короче — события). Например, бросают монету и смотрят, что выпало. В результате этого опыта может выпасть герб—это одно событие, а может выпасть цифра — это другое событие. Поскольку выпадение герба зависит от случая, то это случайное событие. Данная схема содержит как частный случай уже знакомые задачи, имеющие однозначно определенный результат действия.
События принято обозначать буквами А, В, С, ... Например, в опыте с бросанием монеты событие «выпал герб» будем обозначать буквой Г. При этом пишут Г = «выпал герб». Аналогично записывают Ц = «выпала цифра».
Как правило, одна и та же буква может обозначать разные события — надо только каждый раз точно указать, какое именно (подобно тому как при решении геометрических задач буква Aв одной задаче обозначает одну точку, а в другой задаче — другую). Но есть два события, выделяющиеся из массы остальных, за которыми закреплены определенные буквы.
Определение. Событие называется достоверными обозначается буквой Е, если оно обязательно происходит в результате опыта.
Например, в результате бросания монеты обязательно произойдет событие «выпал герб или цифра» — это достоверное событие.
Определение. Событие называется невозможными обозначается буквой U, если оно не может произойти в результате рассматриваемого опыта. Например, при бросании монеты событие «не выпало ни герба, ни цифры» произойти не может — это невозможное событие.
Рассмотрим еще один опыт, более богатый событиями, чем опыт с бросанием монеты, — бросание игральной кости. Он состоит в том, что бросают игральную кость и смотрят, сколько выпало очков При этом могут произойти следующие события:
Q1 = «выпало 1 очко», Q4 = «выпало 4 очка»,
Q2= «выпало 2 очка», Q5= «выпало 5 очков»,
Q3 = «выпало 3 очка», Q6 = «выпало 6 очков».
Но в этом опыте можно рассматривать и другие события, например:
Qпр=«выпало простое число очков»,
Q3к= «число выпавших очков делится на три»,
QЧ= «число выпавших очков четно»,
QН = «число выпавших очков нечетно».
Уже в этом простом опыте мы можем которые типы связей между событиями. Например, события QЧ и QН не могут произойти одновременно. Действительно, число выпавших очков или четно (т. е. произошло событие QЧ), или нечетно (когда произошло событие QН). Этот вид связи между событиями можно наблюдать и в других опытах — он носит определенное название.
Определение. Два события называются несовместными, если они не могут произойти одновременно в рассматриваемом опыте. События, которые в рассматриваемом опыте могут произойти одновременно, называются совместными.
Например, в опыте с бросанием игральное костя события QЧ и Qпрсовместны. Действительно, пусть выпало 2 очка. Число 2 четное; следовательно, произошло событие QЧ. С другой стороны, число 2 простое; следовательно, произошло событие Qпр. Таким образом, события QЧ и Qпр совместны. Аналогично, совместны и события Q3 и Qпр. Однако между совместностью пары событий Q3 и Qпрс одной стороны, и пары событий QЧ и Qпр, с другой стороны, наблюдается существенная разница. Для первой пары из того, что произошло событие Q3, следует, что произошло событие Qпр. Для второй же пары это не так. В самом деле, предположим, что выпало 4 очка, т. е. произошло событие QЧ. Событие Qпр при этом не произошло, так как 4 не является простым числом, т. е. для второй пары из того, что произошло одно из совместных событии, еще не следует, что произошло другое. Таким образом, мы подошли к следующему определению.
Определение. Событие А благоприятствует событию В, если из того, что произошло событие А, следует, что произошло событие В, или пишут: 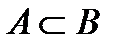 .
.
Так, в опыте с бросанием игральной кости 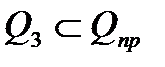 .
.
Для дальнейшего важно отметить следующий факт. В опыте с бросанием игральной кости события Q1, Q2, ..., Q6 выделяются: они попарно несовместны, и в результате опыта одно из них обязательно происходит. Обнаружение подобного множества событий длярассматриваемого опыта весьма существенно при решении вероятностных задач.
Определение. Множество событий рассматриваемого опыта, одно из которых в результате опыта обязательно происходит, а любые два из которых несовместны, называется множеством исходовили полной группой событий этого опыта. Каждое событие из этого множества называется исходомрассматриваемого опыта.
Так, в опыте с бросанием игральной кости события Q1, Q2, ..., Q6 суть исходы этого опыта. Надо подчеркнуть, что для одного и того же опыта можно рассматривать разные множества исходов. Например, для опыта с бросанием игральной кости можно рассматривать множество из двух исходов QЧи QH. В самом деле, эти события несовместны и в результате опыта одно из них обязательно происходит. От того, насколько удачно выбрано множество исходов опыта, зависит большая или меньшая сложность решения поставленной вероятностной задачи: при удачном выборе решение сильно упрощается, а при неудачном или усложняется, или вообще не может быть найдено.
Понятие исходов опыта позволяет установить связь между теорией вероятностей и теорией множеств и придать многим утверждениям большую наглядность. Также как при помощи графика функции просто и наглядно разъясняются многие факты. Начнем с примеров. В опыте с игральной костью любое событие может быть описано множеством исходов этого опыта, благоприятствующих рассматриваемому событию. Например, событие QЧописывается подмножеством исходов {Q2; Q4; Q6},событие Qпр—подмножеством исходов {Q2; Q3; Q5} и т. п. Вместо того, чтобы говорить: событие А = «выпало 3 очка или 5 очков», достаточно указать множество исходов опыта, благоприятствующих событию А, — в нашем случае это {Q3; Q5}.
Аналогичное положение и в общем случае. Каждое событие в рассматриваемом опыте однозначно определяет некоторое подмножество исходов этого опыта. И обратно, каждое подмножество исходов опыта определяет некоторое событие в этом опыте (этому событию благоприятствуют те и только те исходы опыта, которые принадлежит взятому подмножеству). И событие, и подмножество исходов опыта, благоприятствующих этому, событию, мы будем 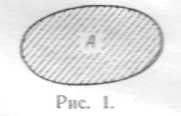 обозначать одной итой же буквой.
обозначать одной итой же буквой.
События будем изображать так же, как в школьном курсе принято изображать множества (рис. 1).
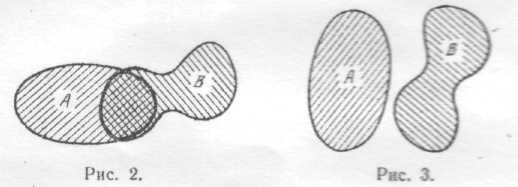
Совместность и несовместность событий легко распознать по графическому изображению (рис. 2 и 3 соответственно). Действительно, на рис. 2 указано, что есть исход опыта, благоприятствующий и событию А, и событию В.Этот исход принадлежит пересечению множеств 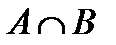 — на рис. 2 оно дважды заштриховано. Если в результате опыта этот исход произошел, то это значит, что произошло и событие А, исобытие В, т. е. эти события совместны. На рис. 3 изображен случай, когда нет исходов опыта, благоприятствующих и событию А,и событию В, т. е. когда эти события несовместны. В самом деле, предположим противное: события Аи В, изображенные на рис. 3, совместны Это значит, что в результате опыта может произойти событие, состоящее в том, что произошло и событие А, и событие В. Этому новому событию благоприятствует некоторый исход опыта (в результате опыта один из исходов обязательно происходит). Этот исход тогда принадлежит пересечению множеств, что противоречит ситуации, изображенной на рис. 3. Полученное противоречие показывает, что сделанное предположение: события Аи В совместны, неверно. Следовательно, события Аи Внесовместны.
— на рис. 2 оно дважды заштриховано. Если в результате опыта этот исход произошел, то это значит, что произошло и событие А, исобытие В, т. е. эти события совместны. На рис. 3 изображен случай, когда нет исходов опыта, благоприятствующих и событию А,и событию В, т. е. когда эти события несовместны. В самом деле, предположим противное: события Аи В, изображенные на рис. 3, совместны Это значит, что в результате опыта может произойти событие, состоящее в том, что произошло и событие А, и событие В. Этому новому событию благоприятствует некоторый исход опыта (в результате опыта один из исходов обязательно происходит). Этот исход тогда принадлежит пересечению множеств, что противоречит ситуации, изображенной на рис. 3. Полученное противоречие показывает, что сделанное предположение: события Аи В совместны, неверно. Следовательно, события Аи Внесовместны.
А какое событие определяется всем множеством исходов опыта? Поскольку в результате опыта один из его исходов обязательно происходит (по определению множества исходов опыта), то множество всех исходов опыта определяет достоверное событие Е. Обычно исходы опыта обозначаются Е1, Е2, …, Еn, поэтому Е= {Е1, Е2, …, Еn}.
А какое событие определяется пустым подмножеством множества исходов опыта? Поскольку в результате опыта один из исходов обязательно происходит, то пустое подмножество исходов опыта, очевидно, определяет невозможное событие U.
2. Алгебра событий. Из школьного курса математики вы знаете, что с множествами можно производить действия — объединения и пересечения. Аналогичные действия мы будем производить и над событиями — это будут те связи между событиями, о которых говорилось в определении теории вероятностей. При этом свойства этих действий будут во многом походить на свойства действий сложения и умножения в алгебре. Это позволит производить вычисления с событиями почти так же, как это делается в алгебре с числами и выражениями, отсюда и название данного раздела — алгебра событий.
 Приведем сначала некоторые разъяснения, подводящие к понятию объединения событий. Рассмотрим два событияAи В. Это два множестваAи Висходов опыта. Объединение этих множеств
Приведем сначала некоторые разъяснения, подводящие к понятию объединения событий. Рассмотрим два событияAи В. Это два множестваAи Висходов опыта. Объединение этих множеств 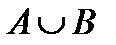 — это некоторое множество исходов опыта, т. е. некоторое событие. Это событие называется объединением событий Аи Ви обозначается
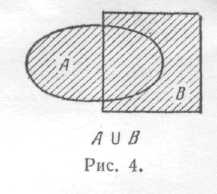
— это некоторое множество исходов опыта, т. е. некоторое событие. Это событие называется объединением событий Аи Ви обозначается 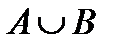 (рис. 4). А как охарактеризовать объединение событий, пользуясь только терминологией теории вероятностей (т. е. терминами «событие произошло» и «событие не произошло»)?
(рис. 4). А как охарактеризовать объединение событий, пользуясь только терминологией теории вероятностей (т. е. терминами «событие произошло» и «событие не произошло»)?
Событию 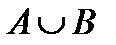 благоприятствуют исходы опыта, которые благоприятствуют хотя бы одному из этих событий (или событиюA, или событию В, или одновременно и событию А, и событию В). Следовательно, событие
благоприятствуют исходы опыта, которые благоприятствуют хотя бы одному из этих событий (или событиюA, или событию В, или одновременно и событию А, и событию В). Следовательно, событие 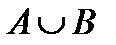 состоит в том, что произошло хотя бы одно из двух событий (или А, или В, или Аи Водновременно).
состоит в том, что произошло хотя бы одно из двух событий (или А, или В, или Аи Водновременно).
Аналогично можно рассматривать объединение любого числа событий. Итак, мы приходим к следующему определению.
Определение. Объединением событий А, В, С… называется событие, состоящее в том, что в результате опыта произошло хотя бы одно из указанных событий. Объединение этих событий обозначается  …
…
Пример 1. Бросается игральная кость. Событие 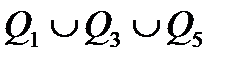 состоит в том, что произошло хотя бы одно из событий Q1, Q3, Q5(выпадение нечетного числа очков). Поэтому можно записать равенство
состоит в том, что произошло хотя бы одно из событий Q1, Q3, Q5(выпадение нечетного числа очков). Поэтому можно записать равенство
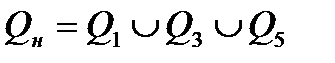 .
.
Определение. Пересечением событий А, В, С, ... называется событие, состоящее в том, что в результате опыта произошли все указанные события. Это событие обозначается  ...
...
Пример 6. Бросили игральную кость. Событие 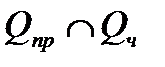 состоит в том, что выпало 2 очка. Это записывается так:
состоит в том, что выпало 2 очка. Это записывается так:
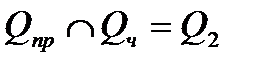 .
.
Пример 9. Если события Аи В несовместны, событие 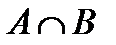 невозможно (события несовместны, если они не могут произойти одновременно в результате опыта). Следовательно, запись
невозможно (события несовместны, если они не могут произойти одновременно в результате опыта). Следовательно, запись 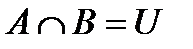
выражает утверждение «события Аи Внесовместны».
Пример 10. Пусть в результате опыта одно из событий A, Вили Сдолжно обязательно произойти. Этозначит, что событие 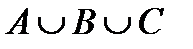 достоверное. Следовательно, запись
достоверное. Следовательно, запись 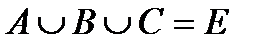 выражает утверждение «в результате опыта обязательно произойдет или событие А, или событие В, или событие С».
выражает утверждение «в результате опыта обязательно произойдет или событие А, или событие В, или событие С».
В алгебре особую роль играют числа 0 и 1. В алгебре событий аналогичную особую роль играют невозможное событие Uи достоверное событие Е(при этом объединение событий аналогично сложению чисел, а пересечение событий аналогично произведению чисел). Равенства в алгебре событий
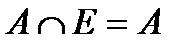 ,
, 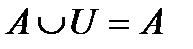 ,
, 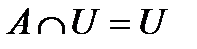
(докажите их самостоятельно) аналогичны, соответственно, алгебраическим равенствам
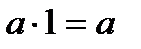 ,
, 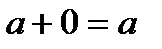 ,
, 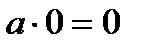 .
.
Наряду с объединением событий рассматривается разность событий.
Определение. Разностьюсобытий A и B называется событие, состоящее в том, что в результата опыта произошло событие Аи не произошло событие В. Обозначается A\В
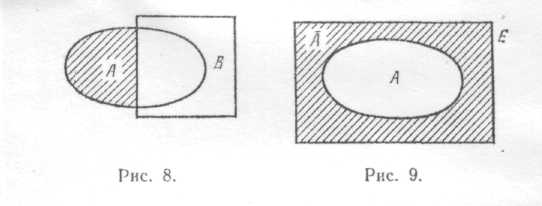
Таким образом, событию A\В благоприятствуют исходы опыта, которые благоприятствуют событию A, но не благоприятствуют событию В. Разность А\Bизображена на рис. 8.
Пример 11. В опыте с бросанием кости
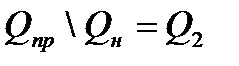 ,
, 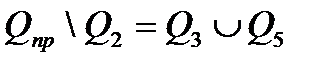 .
.
Пример 12. Пользуясь понятием разности событий, утверждение «событие Ане произошло» можно записать в виде формулы: Е\А. Действительно, любой исход, благоприятствующий событию A, не благоприятствует событию Е\А. Следовательно, если произошло событие Е\А, то событие A не произошло.
При решении многих задач требуется коротко записать «событие A не произошло».
Определение. Событие 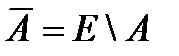 называется противоположнымсобытию A или событием «не А».
называется противоположнымсобытию A или событием «не А».
На рис. 9 заштрихованная фигура изображает coбытие «не A».
Пример 14. В опыте с бросанием кости 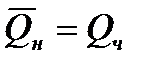 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| ОСНОВЫ МОРСКОЙ ГЕОЭКОЛОГИИ | | | ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД |
Дата добавления: 2021-11-16; просмотров: 732;











