Особенности математической модели процессового перехода с внешним логарифмическим уравнением называемым «эмиссионным уравнением».

Логарифмические уравнения очень не просто решаются. Их приходиться решать на ЭВМ методом подбора. В основном все графические построения выполняются благодаря подпрограмме, способной подбирать решение.

Поэтому, в данном случае, вместе с графиками будут приводиться листинги подпрограмм, обеспечивающие построение этих графиков.

История проблемы.

В 1.1.6. рассматривается математическая модель двухполюсника, состоящего из идеального диода и резистора. Решение для этой модели описывается логарифмическим уравнением, которое решается при помощи подпрограммы подбора решения – Midi.

В 1.1.12.3. выясняется, что тем же уравнением описывается решение для системы с отрицательной обратной связью для экспоненциальной функции. А значит, решается эта задача всё той же подпрограммой Midi и имеет аналогичные графики.

Реальные, существующие кремниевые полупроводниковые диоды при моделировании имеют в качестве модели такое же логарифмическое уравнение. В эмиссионном уравнении для полупроводникового диода имеется только одна отрицательная обратная связь.

Но в эмиссионном уравнении для вакуумного диода, имеется две отрицательные обратные связи. В данном случае можно рассмотреть процессовый переход с внешним логарифмическим уравнением, называемым эмиссионным, где оба процесса будут комплиментарны.

Попробуем изложить математику логарифмических уравнений.

В общем случае эмиссионное уравнение записывается так:

y _рез = exp( K₁∙ (K₂∙z - (x-x₀) ∙ (z-z₀) ))

Для физики процесса : х – это напряжение, z – температура.

K₁ и K₂ - коэффициенты, регулирующие кривизну участка перехода между процессами.

х – аргумент для сигнала прямой связи ( аргумент прямой связи ).

x₀ – аргумент для сигнала обратной связи ( аргумент обратной связи ).

z – аргумент для сигнала прямой связи ( аргумент прямой связи ).

z₀ – аргумент для сигнала обратной связи ( аргумент обратной связи ).

Общий вид эмиссионного уравнения:

y = A = F1(x₀) - функция первого процесса

y = B = F2(z₀) - функция второго процесса

y _рез = exp( K₁ ∙ ( K₂ ∙ z - (x-x₀) ∙ (z-z₀) )) (5.5.2.,01)

Логарифмическое уравнение (5.5.2.,01) является внешней функцией по отношению к функциям A и B. В результате эмиссионное уравнение выглядит так:

_ _

y _рез = exp( K₁∙ ( K₂ ∙z - (x - F1(x) ) ∙ (z – F2(z) ))) (5.5.2.,02)

_ _

где F1(x) и F2(z) - это обратные функции, от первого и второго процесса.

Математическая модель процессового перехода с внешним логарифмическим уравнением называемым «эмиссионным уравнением», для вольт-амперной характеристики прямого тока полупроводникового диода.

Вольт-амперные характеристики полупроводникового диода в условиях изменения температуры ещё нуждаются в изучении. Необходимо в будущем определить физический смысл и физические свойства эмпирических коэффициентов. Кремниевые диоды (как их называют) показывают некоторое совпадение своих вольт-амперных характеристик с эмиссионным уравнением, которое выглядит следующим образом:

_

y _рез = exp( K₁ ∙ ( K₂ ∙z - (x - F1(x) ) ∙ (z – С₁ ) )) (5.5.2.,03)

где С₁ – некоторая константа.

Процесс для переменной z имеет очень малое изменение, потому экспериментально он представляет собой константу С₁ .

Обычно константа С₁ в эмиссионном уравнении обозначается как T_F (температура фокуса) и для кремниевых диодов равна приблизительно 600 Кельвин.

При таких условиях, отсутствует отрицательная обратная связь по отношению к z , и логарифмическое уравнение выражает собой только одну отрицательную обратную связь по отношению к переменной x.

Из 5.3.2 (общий случай обратной связи), делаем вывод, что экспоненциальная функция является внешней, при описании перехода от процесса к процессу.

Уравнение (5.5.2.,03) имеет две переменные, но только одну отрицательную обратную связь. Потому для (5.5.2.,03), процессы относительно x и z не являются комплиментарными.

Преобразуем (5.5.2.,03) следующим образом:

_

y _рез = exp( -K₁∙ (z – С₁ ) ∙ ( (x - F1(x) ) – K₂ ∙ z/( z – С₁ ) ) ) (5.5.2.,04)

Уравнение (5.5.2.,04) отображает влияние параметра z на отрицательную обратную связь, в которую включен параметр x.

Логарифмические уравнения зависят от масштабов функций – процессов. Тем более, если в уравнении присутствуют коэффициенты-регуляторы кривизны переходов между процессами. Потому рассмотрим практический пример – эмпирическое уравнение для вольт-амперной характеристики кремниевого полупроводникового диода КД 213А.

У вольт-амперной характеристики кремниевого полупроводни -кового диода КД 213А есть ряд особенностей, создающих её отличие в физике от эффекта Пельтье.

Так, например вольт-амперная характеристика для прямого тока КД 213А не пересекает ось абсцисс и не пересекает ось ординат. Она, с точки зрения физики, проходит через точку (0,0) согласно закону Ома. Это так называемый «полупроводниковый эффект Пельтье», в котором отсутствует эффект Зеебека (термо-ЭДС ) и отсутствует холодильный эффект Пельтье. То есть, реальность не вписывается в математическую модель и имеет при моделировании ограничивающие условия.

Математическая модель, использующая эмиссионное уравнение имеет диапазон применимости. Она не соответствует физике при значениях аргумента менее 0,1 Вольта для кремниевых диодов.

При значениях аргумента более 0,1 Вольта модель обладает точностью совпадения с экспериментальными данными. Кроме того, её можно сравнить с вольт-амперными характеристиками термопары.

По температуре реальные физические процессы ограничены температурой сверху – для кремния не более 100 градусов по Цельсию. В математической модели, можно наблюдать любые температуры, если это представляет математический интерес.

Общий вид эмиссионного уравнения для кремниевого полупроводникового диода:

y = A = F1(x₀) - функция первого процесса

y = В = F2(x₀) = 0 - функция второго процесса

y _рез = exp( K₁ ∙ ( K₂ ∙ z - (x-x₀) ∙ (z-C₁) ) )

Общий вид эмиссионного уравнения для кремниевого полупроводни- кового диода КД 213А:

Ia = exp( K_T ∙ ( T∙ U_D - (Ua - U_B) ∙ ( Т - T_F ) ) ) (5.5.2.,05)

где:

K_T = 0,0956 Вольт^-1 ∙ Кельвин^-1;

T_F =605,2 Kельвин;

Uv = 0,885 Вольт;

R_D = 0,25 Ом;

U_B = Uv + Ia ∙ R_D или

U_B = 0,885 + Ia ∙ 0,25 ;– обратная функция от функции процесса

U_D = 0,276 Вольт ;

T < T_F .

Функция процесса : Ia = 4∙ (Ua – 0,885) = 4 ∙Ua – 3,54

Ia = (1/ R_D) ∙ ( Ua - Uv )

Учитывая уравнение (5.5.2.,04) можно рассчитать процесс, зависимый от температуры. Это поможет найти процесс как асимптоту ( или похожее на неё ).

_

y _рез = exp( -K₁∙ (z – С₁ ) ∙ ( (x - F1(x) ) – K₂∙z/( z – С₁ ) ) )

Ia = exp( -K_T ∙ ( Т - T_F ) ∙ ( Ua - U_B - T∙ U_D / ( Т - T_F ) ) ) (5.5.2.,06)

То:

U_B + U_D∙T/( Т - T_F ) = 0,885 + Ia∙ 0,25 + 0,276∙ T/( Т - T_F )

Отсюда:

Ua = Uv + Ia∙ R_D + U_D∙ T/( Т - T_F )

Ia = ( 1/ R_D ) ∙ ( Ua – Uv –U_D∙ T/( Т - T_F ) (5.5.2.,07)

Ia = 4∙ (Ua -0,885 – 0,276∙ T/( Т - T_F ) ) = 4∙Ua – 3,54 - 1,104∙ T/( Т - T_F )

На рисунке 5.19. построим график функции для температуры 20 градусов по Цельсию . Тут же построим график для функции

F3(Ua) = Ia = 4∙Ua – 3,54 - 1,104∙ T/( Т - T_F ).

Функция F3(Ua) является расширенной функцией процесса A.

Она состоит из трёх слагаемых. Ток отрицательной обратной связи состоит из 3 –х составляющих:

+ 4∙Ua – это ток ООС при проводимости 4 Сименс.

– 3,54 Ампер – постоянная составляющая

- 1,104 ∙ T/( Т - T_F ) Ампер – температурная составляющая .

Рис. 5.19. График, иллюстрирующий одномерный процессовый переход. Н на графике построены функции: для процесса A =F3(Ua) = Ia = ( 1/ R_D ) ∙ ( Ua – Uv –U_D∙ T/( Т - T_F ), и процесса B = Ia = 0, и построена функция Ia _рез = exp( -K_T∙ ( (Ua - U_B) ∙ ( Т - T_F ) - T∙ U_D ) ) . Ось абсцисс в Вольтах, ось ординат в Амперах.

Подпрограмма, вычисляющая функцию Ia _рез :

procedure MidI3_4(x,z:real;var y:real;var c0:integer);

var

Ymax, Ymin, X0, E: real;

Kt,Ub,Ud,Uf,Tf:real;

A,B,C,D:real;

begin

c0:=0;

E:=0.000001;

Tf:=605.2;

Ud:=0.276;

Kt:=0.0956;

Ymax:=exp(((Tf-z)*x + z*Ud)*Kt);

Ymin:=0;

repeat

begin

y:=(Ymax+Ymin)/2;

Ub:= 0.885+ y*0.25; // обратная функция для x

Uf:=Ub+Ud;

if y<=0 then

begin

c0:=1; // код ошибки

break;

end;

A:=Ln(y);

B:=A/(-Kt);

C:=B+z*Ud;

D:=z-Tf;

if D=0 then

begin

c0:=2; // код ошибки

break;

end;

X0:=(C/D)+Ub; // поэтапное вычисление х ( или Ua )

if X0 > x then Ymax:=y else Ymin:=y;

end until (X0+E > x) and (X0-E < x);

end;

На графике на рисунке 5.19. видно, что процесс А не является асимптотой. Во всяком случае, это надо доказать. Логарифмические уравнения зависят и от алгоритма вычисления. Алгоритм также надо проверять на ошибки. У полупроводникового диода тепловой и электрический процесс не обладают комплиментарностью.

Рассмотрим несколько примеров моделирования комплиментарных процессов при помощи эмиссионного уравнения.

Математическая модель процессового перехода с внешним логарифмическим уравнением называемым «эмиссионным уравнением», для вольт-амперной характеристики вакуумного диода с вольфрамовым катодом.

Здесь мы можем рассмотреть уже знакомый нам эксперимент С. Дэшмана.

Общий вид эмиссионного уравнения:

y = A = F1(x₀) - функция первого процесса

y = B = F2(z₀) - функция второго процесса

y _рез = exp( K₁∙ ( K₂∙z - (x-x₀) ∙ (z-z₀) ) ) (5.5.4.,01)

Для физики процесса : х – это напряжение, z – температура.

K₁ и K₂ - коэффициенты, регулирующие кривизну участка перехода между процессами.

х – аргумент для сигнала прямой связи ( аргумент прямой связи ).

x₀ – аргумент для сигнала обратной связи ( аргумент обратной связи ).

z – аргумент для сигнала прямой связи ( аргумент прямой связи ).

z₀ – аргумент для сигнала обратной связи ( аргумент обратной связи ).

Логарифмическое уравнение (5.5.4.,01) является внешней функцией по отношению к функциям A и B.

В результате эмиссионное уравнение выглядит так:

_ _

y _рез = exp( K₁∙ ( K₂ ∙z - (x - F1(x) ) ∙ (z – F2(z) ) ) ) (5.5.4.,02)

_ _

где F1(x) и F2(z) - это обратные функции, от первого и второго процесса.

Первый процесс – электрический - это «закон 3/2». Он так и представлен в модели, но имеет эмпирический вид:

F1(Ua) = Ia = 9,215∙10^-5 ∙ Ua ^3/2

где

Ia – ток анода в Амперах,

Ua – напряжение на аноде в Вольтах.

Обратная функция будет иметь вид:

__

F1(Ua) = U_B = ( Ia / 9.215∙10^-5) ^2/3 (5.5.4.,03)

Второй процесс - тепловой имеет эмпирический вид:

F2(T) = Ia = exp( 1,047∙10^-2 ∙ T - 27,325 )

где

Ia – ток анода в Амперах,

T - температура катода в Кельвинах.

Обратная функция будет иметь вид:

__

F2(T) = T_F = (Ln ( Ia) +27,325 ) / 1,047∙10^-2 (5.5.4.,04);

Составим эмиссионное уравнение.

y = A = F1(Ua) = - функция первого процесса

y = B = F2(T) - функция второго процесса

y _рез = exp( K₁ ∙ ( K₂ ∙T - (Ua-U_B) ∙ (T-T_F) ) )

Определим K₁ как К_T

Определим K₂ как U_D

Далее следует:

Ia = exp ( K_T ∙ ( T∙ U_D - ( T - T_F ) ∙ (Ua - U_B) ) ) (5.5.4.,05)

K_T = 0,0956 Вольт^-1 ∙ Кельвин^-1;

T_F =(Ln ( Ia) +27,325 ) / 1,047∙10^-2 ;

U_B = ( Ia / 9,215∙10^-5) ^2/3 ;

U_D = 0,01 Вольт;

T > T_F .

K_T и U_D - коэффициенты, регулирующие кривизну участка перехода между процессами.

T_F и U_B - обратные функции процессов A и B.

На основе соотношения (5.5.4.,05), применяя подпрограмму Midi, можно построить графики вольт-амперных и кельвин-амперных характеристик. На рисунке 5.20. представлен график с аргументом Ua.

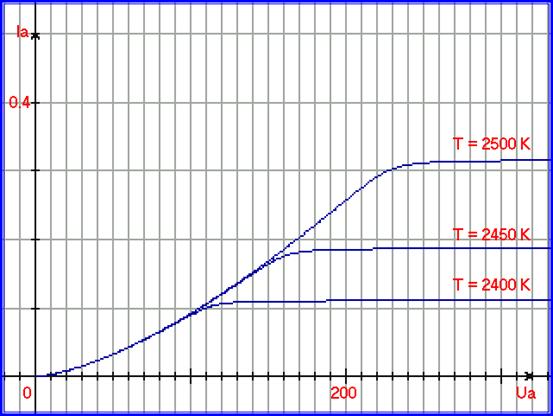
Рис. 5.20. График, иллюстрирующий двухмерный процессовый переход. Для процессов Ia=A = F1(Ua) = 9.215∙10^-5 ∙ Ua ^3/2,

и Ia = B= F2(T) = exp( 1.047∙10^-2 ∙ T - 27.325 ),