Внешняя степенная функция процессового перехода. Показатель степени как регулятор кривизны переходного участка.

Для плавного регулирования изгиба перехода от функции A к функции B удобно использовать степенную функцию.

Преобразуем знаменатель уравнения «весов» по правилу, записанному в (5.2.3.,02). В таком случае F – это степенная функция.

У = F(x) = x^N, где N – действительное число.

Уравнение процессового перехода с регулируемой кривизной переходного участка будет выглядеть так:

y = A = F1(x)

y = B = F2 (x)

_N _____________

y_рез = A∙B / √ A^N + B^N (5.2.4.,01)

Как было сказано, уравнение такого типа создаёт переход от процесса к процессу по принципу приближения к минимуму от этих двух процессов.

Посмотрим на нескольких графических примерах, как работает уравнение «весов» на основе степенной функции.

На рисунке 5.5. построим процессовый переход по уравнению «весов» на основе степенной функции с показателем степени N=3 между функциями:

y = x² и y = 0,2 ∙ x + 50 .

Процессовый переход будет выражаться следующей системой уравнений:

y = A = F1(x) = x²

y = B = F2 (x) = 0,2 ∙ x + 50

_N ____________

y_рез = A∙B / √ A^N + B^N

N = 3

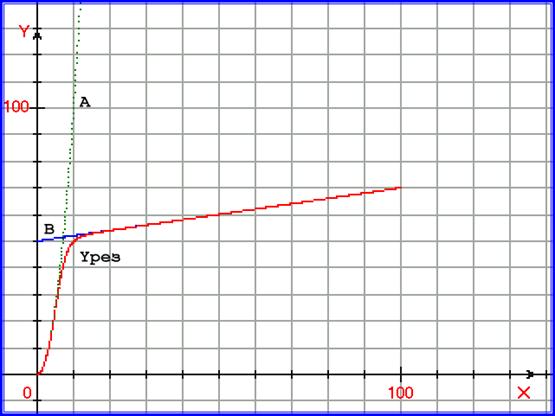
Рис. 5.5. График, иллюстрирующий одномерный процессовый переход. На графике построены функция y=A = x², функция y = B= 0,2∙x+50, и функция y_рез =A∙B/ (A ^N+B^N) ^1/N , при N =3.

На рисунке 5.6. построим процессовый переход по уравнению «весов» на основе степенной функции с показателем степени N=10 между функциями:

y = x² и y = 0,2 ∙ x + 50 .

Процессовый переход будет выражаться следующей системой уравнений:

y = A = F1(x) = x²

y = B = F2 (x) = 0,2 ∙ x + 50

_N ___________

y_рез = A∙B / √ A^N + B^N

N = 10

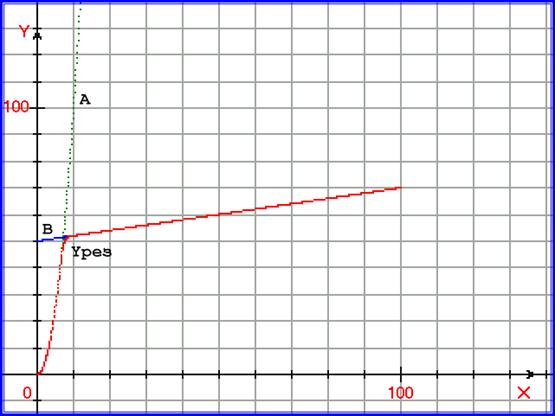
Рис. 5.6. График, иллюстрирующий одномерный процессовый переход. На графике построены функция y=A = x², функция y = B= 0,2∙x+50, а также функция y_рез =A∙B/ (A ^N+B^N) ^1/N , при N =10.

На рисунках 5.4., 5.5., 5.6. видно, что изменяя величину N, мы можем регулировать кривизну участка перехода от процесса к процессу. На рисунке 5.6. можно наблюдать, что функция Yрез, почти сливается с частью параболы и прямой, а сам участок перехода очень резкий.