Уравнение обратной связи для степенной функции. ООС.

Рассмотрим степенную функцию, при отрицательной обратной связи. Нахождение решения для степенной функции аналитическим способом довольно сложно. Степенная функция:

y = xⁿ ;

Обозначим степенную функцию как y =Fs(x) .

Рассмотрим степенную функцию, при отрицательной обратной связи (согласно рисунку 1.27.).

η=dy/y - коэффициент обратной связи ( блок 1)

где dy - количество выходного сигнала, подаваемого на входной сумматор.

p=- η ∙ y - функция обратной передачи ( блок 1)

y= Fs ( s ) - функция прямой передачи ( блок 3)

p=- η ∙ y - отрицательная обратная связь.

s=x+p - функция сумматора (блок 2)

s= x- η ∙ y ;

отсюда

y = Fs ( x - η ∙ y ) ; (5.3.1.,01)

В результате получается уравнение (5.3.1.,01), решаемое с помощью подпрограммы MidI_S01 с применением ЭВМ. Подпрограммы, подобные MidI_S01 могут решать задачи для расчёта ООС.

001 procedure MidI_S01(x,n1,r1:real;var y:real);

002 var

003 Imax, Imin, x0, E: real;

004 begin

005 E:=0.00001;

006 Imax:= power(x,n1);

007 Imin:=0;

008 repeat

009 begin

010 y:=(Imax+Imin)/2;

011 x0:=power( y ,1/n1 ) + r1*y;

012 if x0 > x then Imax:=y else Imin:=y;

013 end until (x0+E > x) and (x0-E < x);

014 end;

В подпрограмме:

В строке 6 функция y = xⁿ обозначена как power(x,n1).

n1 – показатель степени;

r1 – коэффициент обратной связи;

Строка 6 – это максимальное значение, от которого начинается поиск решения – это вход в цикл подпрограммы.

Строка 11 – это выражение, рассчитывающее x.

Подпрограмма MidI_S01 разработана для одной входной переменной (в данном случае - x). Функция, для которой ведётся поиск решения, должна быть монотонной, возрастающей.

Приведём несколько примеров ООС для нескольких степенных функций. Решение для ООС степенных функций найдено при помощи подпрограммы MidI_S01. Эта подпрограмма может вычислять результат обратной связи для функций – чёрных ящиков.

На рисунке 5.9. построим степенную функцию y = x⁵ , а также поверх неё функцию y =( x – 0,001 ∙ у )⁵ .

На рисунке 5.10. построим степенную функцию y = x^0.5 , а также функцию y =( x – 0,99 ∙ у )^0.5 .

Линейная функция y = x¹ является частным случаем степенной функции.

На рисунке 5.11. построим степенную функцию y = x¹ , а также функцию y =( x – 0,99 ∙ у )¹ .

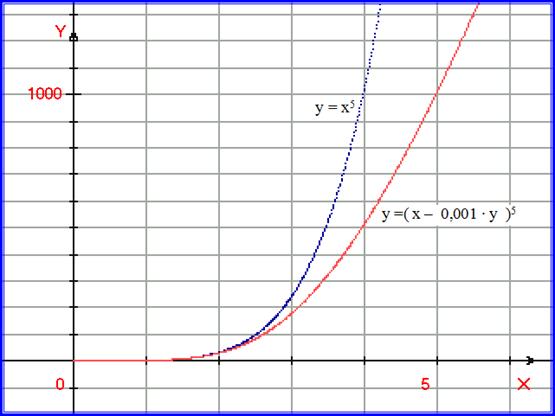
Рис. 5.9. На графике построены: степенная функция y = x⁵ , а также функция y =( x – 0,001∙у )⁵ .

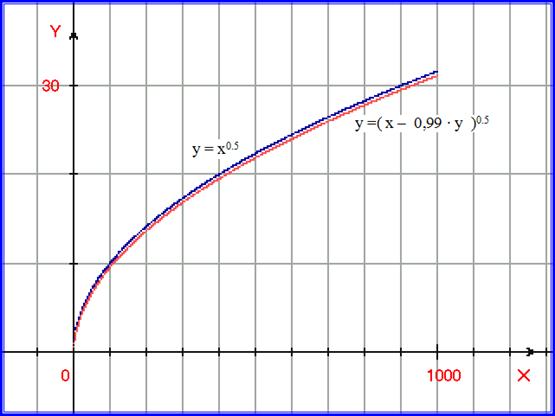
Рис. 5.10. На графике построены: степенная функция y = x^0.5 , а также функция y =( x – 0,99∙ у )^0.5 .

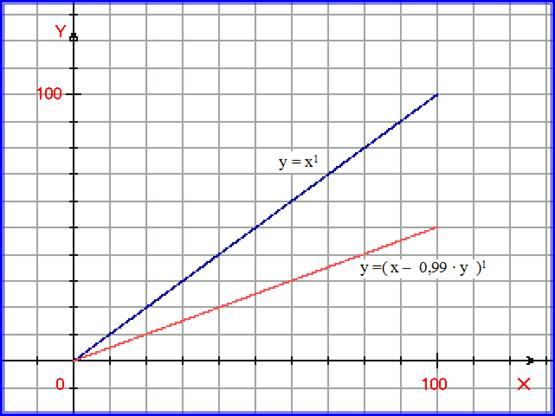
Рис. 5.11. На графике построена степенная функция y = x¹ , а также функция y =( x – 0,99∙ у )¹ .