Математическая модель процессового перехода с внешней степенной функцией для вольт-амперной характеристики вакуумного диода с вольфрамовым катодом.

Задача моделирования заключалась в том, чтобы создать модель для эксперимента С. Дэшмана. Описание приведено в 2.1.1.

Автор эксперимента указывал, что две функции ограничивают рост друг друга. Это значит, что можно создать модель с двумя процессами – тепловым и электрическим, в которых присутствует две независимых отрицательных обратных связи. Рассмотрим эти два процесса: явление насыщения анодного тока – закон Ричардсона-Дэшмана и явление ограничения анодного тока Объёмным Пространственным Зарядом – «закон 3/2».

Уравнение Ричардсона – Дэшмана, описывающая первый из этих процессов - в современной физике основывается на квантовой механике и её можно найти в источниках.

В своей модели вместо уравнения Ричардсона-Дэшмана я использовал более простой выражения этой взаимосвязи. При исследовании этой зависимости, было замечено, что функция имеет вид экспоненты. Поэтому функция теплового процесса имеет эмпирический вид ( эмиссионное уравнение):

Ia = exp( 1.047∙10^-2 ∙ T - 27.325 )

где

Ia – ток анода в Амперах,

T - температура катода в Кельвинах.

Второй процесс – электрический - это «закон 3/2». Он так и представлен в модели, но имеет эмпирический вид:

Ia = 9.215∙10^-5 ∙ Ua ^3/2

где

Ia – ток анода в Амперах,

Ua – напряжение на аноде в Вольтах.

Первый вариант модели создавался по уравнению «весов» с использованием внешней степенной функцией. Для выполнения условия совпадения переходного участка использовался показатель степени N = 5.

Модель выглядела так:

Процессовый переход будет выражаться следующей системой уравнений:

Ia = A = F1(Ua) = 9.215∙10^-5 ∙ Ua ^3/2

Ia = B = F2 (T) = exp ( 1.047∙10^-2 ∙ T - 27.325 )

_N _________________

Ia _рез = A ∙ B / √ A^N + B^N

N = 5

Так, как переменных две, то можно построить 2 семейства характеристик. На рисунке 5.17. представлен график с аргументом Ua.

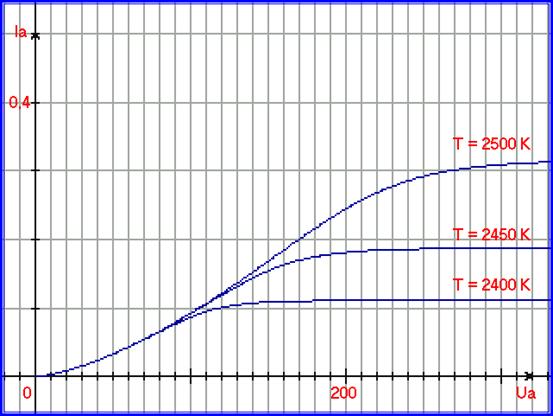
Рис. 5.17. График, иллюстрирующий двухмерный процессовый переход. Для процессов Ia=A = 9,215∙10^-5 ∙ Ua ^3/2, и Ia = B= exp( 1,047∙10^-2 ∙ T - 27,325 ), построена функция Ia _рез =A∙B/ (A ^N+B^N) ^1/N , с аргументом Ua при 3-х температурах, при N =5. Ось абсцисс в Вольтах, ось ординат в Амперах.

На рисунке 5.18. представлен график с аргументом T.

Рис. 5.18. График, иллюстрирующий двухмерный процессовый переход. Для процессов Ia=A = 9,215∙10^-5 ∙ Ua ^3/2, и Ia = B= exp( 1,047∙10^-2 ∙ T - 27,325 ), построена функция Ia _рез =A∙B/ (A ^N+B^N) ^1/N , с аргументом T при 10-ти значениях Ua, при N =5. Ось абсцисс в Кельвинах, ось ординат в Амперах.

1 . Наблюдение 1-е: что две отрицательные связи существуют независимо друг от друга.

2. Наблюдение 2-е: процессы ограничивают рост друг друга.

Более подробно: при изменении одного процесса, происходит или ограничение другого процесса или ограничение смещается, тем самым - у другого процесса возникает возможность роста.

3. Наблюдение 3-е: процессы ( две функции ) являются асимптотами. Для графиков на рис. 5.17. и 5.18. видно, что каждый график представлен функцией, переходящей от первого процесса к некоторой ограничивающей прямой, параллельной оси абсцисс. Эта прямая и отображает второй процесс и является ограничивающей.

Можно сделать вывод, что отрицательная обратная связь, существующая для двух переменных, представляет собой двухмерный процессовый переход, где два процесса ограничивают рост друг друга.

Процессы (функции), существующие в условиях одного явления (двухмерного процессового перехода) называются комплиментарными, если рост одного процесса позволяет расти второму процессу и наоборот.

Двухмерный процессовый переход, где два процесса ограничивают рост друг друга, обладает комплиментарными процессами.