Вектор функция. Параметрическая производная.
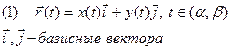
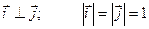
По закону (1) ставиться в соответствие вектор r(t). (x(t),y(t) – заданные числовые функции
r(t) – вектор функция. Кривая описываемая концом вектора – называется годографом.
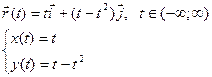
| t | -1 | ½ | ||||
| x(t) | -1 | ½ | ||||
| y(t) | -2 | -2 | -6 | 1/4 | ||
| r(t) | i | -i-2j | 2i-2j | 3j-6j | 1/2i+1/4j |
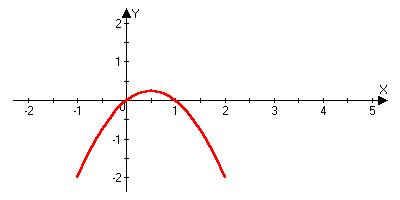
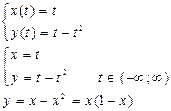
Видим, что кривые на плоскости можно задать в виде:

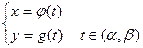 Называется параметрическое задание кривой, где t –параметр
Называется параметрическое задание кривой, где t –параметр
x2+y2=r2
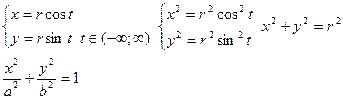

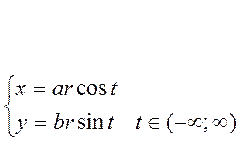
Остроида
x2/3+y2/3=a2/3

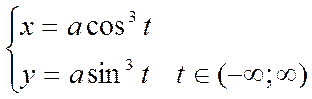
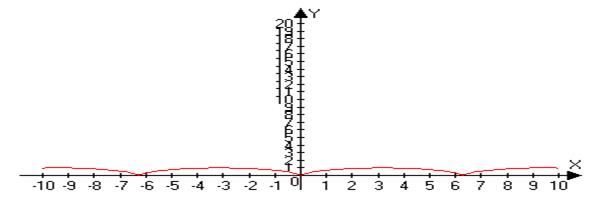
Циклоида
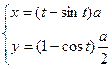
[1] На концах отрезка [a,b] и на концах принимает значение разных знаков
[2] a(x-x0)-бесконечно малое при х®х0
1 x¹0
1 a(∆x) – бесконечно малое при ∆х®0, а a(∆x)∆х – есть о∆х
1 Y – ордината касательной
a – x-x0 =∆x
1 ∆-погрешность вычисления.
Теорема –Если f(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), то $ сÎ(a,b): f(b)-f(a)=f(c)(b-a)
1 (x-x0)=∆x
1 Теорема – Если f(x) непрерывна на [a,b] дифференцируема на отрезке (а,b), то $ сÎ(a,b): f(b)-f(a)=f(c)(b-a)
II – g’(c1)=0 по условия теоремы
III – (b-a)=0
4 - Теорема (Ролля): Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда $ сÎ(a,b): f(c)=0
1 0((x-x0)n)(x-x0) – остаточный член в форме пеано
ii a(х-х0) – бесконечно малое при х®х0
* o’º1 x2n+2=x·x2n+1=o(x2n+1)
# 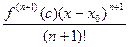 - остаточный член в форме Лангранджа
- остаточный член в форме Лангранджа
$ -Tn(x) – многочлен Тейлора
§ Rn(x)-остаточный член в форме Лангранджа
Дата добавления: 2016-07-22; просмотров: 2100;











