Дифференциал функции.

Определение: Пусть y=f(x) определена в некоторой О(х₀) – она называется дифференцируемой в точке х₀, если её приращение в этой точки представимо в виде:

∆y=∆f(x₀)=A∆x+a(∆x)∆x)1

a(0)=0 A=const

Определение: линейная ∆х часть приращение дифференцируемой функции называется дифференциалом функции в точке х₀:

dy=df(x₀)ºA∆x

Теорема: Если функция дифференцируема в точке х₀ то A=f’(x₀), то она имеет производную в этой точке, то A=f’(x₀); наоборот если функция имеет производную в этой точке, то она дифференцируема в этой точке – называется дифференциалом.

Доказательство:Пусть y=f(x) дифференцируема в точке х₀, то есть в некоторой О(х₀) справедливо равенство ∆f(x₀)=A∆x+a(∆x)∆x¹; a(0)=0. Поделим обе части этого равенства на ∆х и приведём к пределу при ∆х®0:

lim(∆f(x₀))/∆x=lim(A+a(x))=A. Этот предел существует, меньше ¥, тогда по определению этот предел есть

^{∆x®0 ∆x®0}

производная.

Доказательство: (в обратную сторону) Пусть в точке х₀ $ f’(x₀)(<¥) – это означает, что f(x) определена в некоторой О(х₀) и $ lim(∆f(x₀))/∆x=f’(x₀)Þ по определению предела следует, что в некоторой О(х₀)

^∆x®0

(∆f(x₀))/∆x=a(∆х)+f’(x₀) при ∆х®0 Þ ∆f(x₀)=f’(x₀)+a(∆x)∆x, так как lima(∆x)=0, то в точке х₀ y a(∆x) может

^∆х®0

быть лишь устранимым разрывом . Устраним его, определим и доопределим:

a(0)=0, тогда ∆f(x₀)=f’(x₀)∆x+a(∆x)∆x Þ A=f’(x₀) из установленного соответствия получим выражения для дифференцируемой функции df(x₀)=f’(x₀)∆x

Следствие: по определению полагают дифференциал независимой переменной равной её приращению

dx=∆x (х - независимая переменная)

df(x)=f’(x)dx

f(x)=x – вычислим дифференциал f’(x)=1 df(x)=dx=f(x)∆x=1∆x

Замечание: дифференциал функции зависит от двух переменных – от самой точки х и от ей приращения

y=cosx x₀=p/2 ∆x=p/180

y’=-sinx y’(p/2)=-sin(p/2)=-1

dy(p/2)=-1∆x=-1p/180=-p/180

Теорема: Пусть y=f(x) дифференцируема в точке х₀, а z=g(y) дифференцируема в точке у₀=f(x₀), тогда сложная функция z=g(f(x) - дифференцируема в точке х₀ и z’(x₀)=g’(f)f’(x)

Доказательство: (1) ∆z=g’(y₀)∆y+a(∆y)∆y

(2) ∆y=f(x₀)∆x+b(∆x)∆x a(0)=0 b(0)=0

Подставим в первое равенство второе:

∆z=g’(y₀)f(x₀)∆x+g’(y₀)b(∆x)∆x+a[f’(x₀)+b(∆x)∆x][f’(x₀)∆x+b(∆x0∆x]

lim∆z/∆x=limg’(x₀)f’(x₀)+limg’(x₀)b(∆x)+lim a(f’(x₀)+b(∆x)∆x)[f’(x₀)+b∆x] Þ z’(x₀)=g’(y₀)f’(x₀) что и требовалось

^{∆x®0 ∆x®0 ∆x®0 ∆x®0}

доказать.

Теорема: Пусть функция y=f(x) возрастает (убывает) в О(х₀) и дифференцируема в точке х₀. Тогда обратная у ней функция x=g(y) дифференцируема в точки y₀=f(x₀), причём g’(y₀)=1/f(x₀)

Доказательство: из дифференцируемой функции f(x) в точке х₀ и из монотонности следует существование обратной функции в точке х₀ и её непрерывность lim[∆y(y₀)]/∆y= ∆y®0, то ∆у¹0 Û в силу строгой

^∆у®0 монотонности функции и обратной =

к ней следует ∆х¹0

=lim∆x/∆y=lim1 /(∆y/∆x)= в силу непрерывности следует =1/[lim∆y/∆x]=1/[lim∆f(x₀)/∆x]=1/f(x₀) f(x₀)¹0

^{∆y®0 ∆y®0} ∆у®0, то ∆х®0 и наоборот ^{∆x®0 ∆x®0}

y=a^x

y’(x)=lim[a^x+∆x-a^x]/∆x=lim[a^x(a^∆x-1)]/∆x=lim[a^x(e^∆xlna-1)]/∆x=/∆x®0, то ∆xlna®0\=lim[a^x∆xlna]/∆x=a^xlna

^{∆x®0 ∆x®0 ∆x®0 ∆x®0}

y’=a^xlna, частный случай y=e^x Þ (e^x)’=e^x

^{y=x^2}

_{y’=x^2 lnx}

y=lnx

y’=lim[ln(x+∆x)-lnx]/∆x=lim[ln((x+∆x)/x)]/∆x=lim[ln(1+∆x/x)]/∆x=/∆x/x®0 при ∆x®0\=lim(∆x/x)/∆x=1/x

^{∆x®0 ∆x®0 ∆x®0 ∆x®0}

(lnx)’=1/x

^y=lnx

_y’=1/x

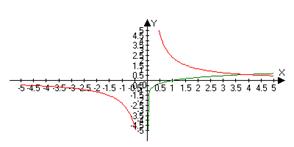y=log_ax=lnx/lnaÞ (log_ax)’=1/xlna

^y=lgx

_y’=1/xln10

y=arcsinx обратная функция x=siny xÎ[-1;1] yÎ[-p/2;p/2]

(arcsinx)’|_x=x0=1/(siny)’|_y0=y=1/cosy|_y0=y=

yÎ[-p/2;p/2], cosy³0 cosy>0, если yÎ[-p/2;p/2] то есть x¹±1

=1/Ö(1-sin²y)|_y=y0=1/Ö(1-(sinarccosx)²)|_x=x0=1/Ö(1-x₀²)

(arcsinx)’=1/Ö(1-x²)

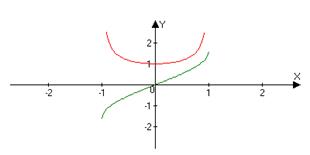^y=arcsinx

_{y’=1/Ö(1-x^2)}

y=acrcosx, обратная x=cosy xÎ[-1;1] yÎ[0;p]

(arcosx)’=1/(cosy)’|_y=y0=1/-siny|_y=y0=-1/Ö(1-cos²y)|_y=y0=-1/Ö(1-(cosarccosy)²)|_x=x0=-1/Ö(1-x₀²)

(arcosx)’=-1/Ö(1-x²)

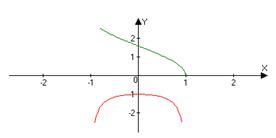
^y=arccosx

_{y’=--1/Ö(1-x^2)}

y=arctgx обратная функция x=tgy yÎ(-p/2;p/2)

(arctgy)’=1/(tgy)’=cos²y= / 1+tg²y=1/cos²y \ =1/(1+x²)

(arctgy)’=1/(1+x²)

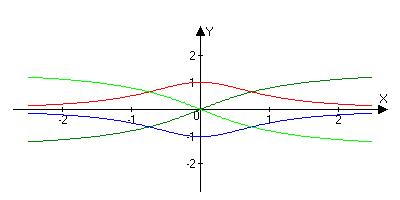(arcctgy)’=-1/(1+x²)

^y=arctgsx

_{y’=-1/ (1+x^2)}

^y=arcctgx

_{y’=--1/ (1+x^2)}