Применение формулы Тейлора с остаточным членом в форме Лангранджа.
Пусть функция f(x) – два раза дифференцируема в О(х0), тогда
 f(x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2 где с лежит между х и х0
f(x)=f(x0)+f’(x0)(x-x0)+[f’’(c)(x-x0)2]/2 где с лежит между х и х0
уравнение касательной
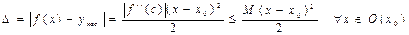
Если |f’’(x)|£M "xÎO(x0)
f(x)-n+1 – дифференцируема в О(х0)
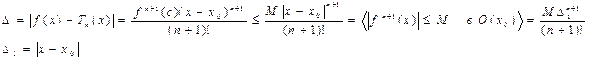
f(x)=Tn(x)+Rn(x)§ в О(х0)
n=1
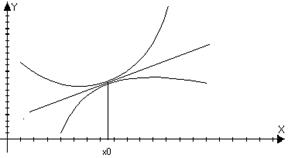 T1(x) – линейная функция
T1(x) – линейная функция
n=2
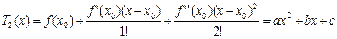
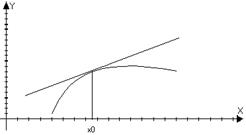
- график парабола
|f(x)-T1(x)|=|f’(x0)||x-x0|
|f(x)-T2(x)|=[|f’’(x0)||x-x0|2]/2
T3(x)=ax3+bx2+cx+d – график кубическая парабола
 Выпуклость и вогнутость.
Выпуклость и вогнутость.
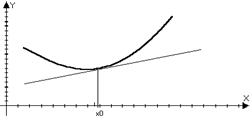
Определение: Пусть функция f(x) – дифференцируема в
точке х0, то она называется выпуклой (вогнутой) в верх
в точке х0, если f(x)-yкас<0 в О(х0)
 |
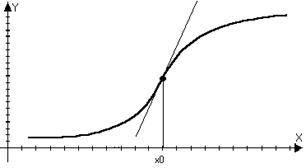
Определение: Пусть функция f(x) – дифференцируема в
точке х0, то она называется выпуклой (вогнутой) вниз в
точке х0, если f(x)-yкас>0 в О(х0)
 |
Определение: Пусть функция f(x) – дифференцируема в
точке х0, то она называется выпуклой (вогнутой) в верх
(вниз) на интервале (a,b), если она выпукла в верх (вниз)
в каждой точке этого интервала.
Определение: (точки перегиба) Пусть функция f(x) диф-
ференцируема в О°(х0) и непрерывна в О(х0). Точка х0 –
называется точкой перегиба графика f(x), если при пере-
ходе через точку меняется знак выпуклости.
Теорема: (о достаточном условии выпуклости функции).
Пусть функция f(x) дважды дифференцируема в точке х0 и f’’(x0)<0 (f’’(x0)>0), тогда f(x) – выпукла вверх (вниз) в тоске х0.
Доказательство: Напишем формулу Тейлора с остаточным членом в форме пеано:
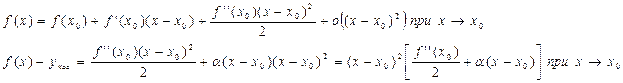
Если х близко к х0, то знак квадрата скобки определяется знаком f(x0). Если f’’(x0)<0, то f(x)-yкас>0 в О°(х0).
Если f’’(x0)>0, то f(x)-yкас>0 в О°(х0)
Теорема: Путь функция f(x) непрерывна в О(х0) и дважды дифференцируема в О°(х0), причём f’(x) меняет знак при переходе через точку х0, тогда точка х0 – точка перегиба.
Доказательство:
f’’(x) - +
 ( · ) x
( · ) x
x0
f’’(x)<0 в O°-(x0)Þ f(x) – выпукла вверх в О°-(х0)
f’’(x)>0 в O°+(x0)Þ f(x) – выпукла вниз в О°+(х0)
Следствие: Если f(x) дважды дифференцируемы в точке х0. Если точке х0 точка перегиба, то f’’(x0)=0
Путь точка х0 точка перегиба и существует f’’(x0)>0, тогда
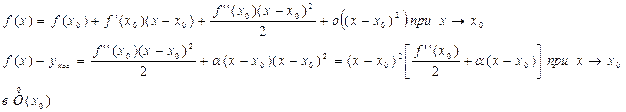
то есть при переходе через точку х0 левая часть равенства f(x)-yкас не меняет знак. Аналогично получаем для f(x)>0 f’’(x0)=0
Замечание: Условие равенства f’’(x0)=0 необходимо, но недостаточно.
Теорема: (о достаточном условие экстремума по второй производной)
Пусть функция f(x) дважды дифференцируема в точке х0, тогда точка х0 точка максимума если f’’<0, точка х0 точка минимума если f’’(x0)>0.
Доказательство:

При х достаточно большим и х0 знак в квадратных скобках совпадает со знаком f’’(x0)Þ f(x)-f(x0)>0 в О°(х0), если f’’(x0)>0 то есть f(x)>f(x0) в О°(х0)Þ х0 точка минимума, если f(x)-f(x0)<0 в О°(х0), и если f’’(x0)<0 то есть f(x)<f(x0) в О°(х0)Þ х0 точка максимума.
Замечание: Если f’(x0)=0 и f’’(x0)=0, то нужны дополнительные исследования.
Лекция №17
Дата добавления: 2016-07-22; просмотров: 2276;











