Экстремумы функции.

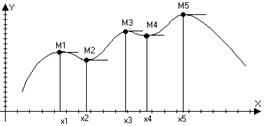Можно указать О(х₁) в которой все значения функции

f(x)<f(x₁) b и О°_d1(х₁) анологично для точки х₂

f(x)>f(x₁) b и О°_d2(х₁). Значенгие функции в точке М₁, М₃ и М₅ –

max; M₂ и М₄ – min – такие точки назавыются точкками

экстремума или точками локального max и min.

Определение: (точки экстремума)

Пусть функия f(x) определена в некоторой О(х₀) и f(x)>f(x₀) в

О°(х₀) или f(x)<f(x₀) в этом случае точка х₀ – называется точкой локального max (min).

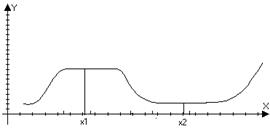Замечание:

f(x)£f(x₁) в О_d1(х₁)

f(x)³f(x₂) в О_d2(х₂)

говорят, что точки х₁ и х₂ точки не строгого локального

экстремума.

Теорема: (Ферма) (о необходимости условия экстремума дифференцируемой функции)

Пусть y=f(x) дифференцируема в точки х₀ и точка х₀ – точка экстремума, тогда f(x₀)=0

Доказательсто: Заметим, что х₀ точка экстремума, то в её окрестности f(x) – f(x₀) сохраняет знак. Запишем условие ∆f(x₀)=f(x)-f(x₀)(x-x₀)+o(x-x₀)

f(x)-f(x₀)=(x-x₀)[f(x₀)+a(x-x₀)] то при х – достаточно близких к х₀ знак выражения стоящего в квадратных скобках совпадает со знаком f’(x₀)¹0 (x-x₀) – меняет знак при переходе черех точку х₀ Þ f’(x₀)=0

Лекция №13

Тема: «Экстремумы»

Замечание:

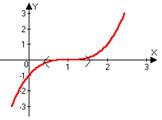Обратное утверждение неверно. Из-за того, что произведение в данной точки равно нулю, не следует, что это экстремум.

y=(x-1)³

y’=3(x-1)²

y’(1)=0

x₀=1

xÎO°^-_d(1)Þf(x)<0

xÎO°⁺_d(1)Þf(x)<0

x=1 – не точка экстремума.

Теорема (Ролля):

Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда $ сÎ(a,b): f(c)=0

Доказательство: Така как функция непрерывна на отрезке [a,b], то по второй теореме Вейштрасса есть наибольшее и наименьшее значение (m,M), если m=M, то f(x)ºconst ("xÎ[a,b]) (const)’=0.

Пусть m<M, тогда либо m, либо М отлична от значений на концах отрезка. Пусть например M¹f(a):$ c(a,b):f(c)=M, то есть точка с точка экстремума максимума следовательно по теореме Ферма f’(c)=0

Замечание: условие дифференцируемсти нельзя отбросить.

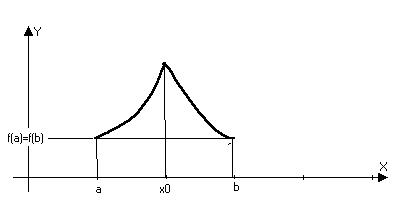
непрерывна на отрезке [a,b]

Геометрический смысл.

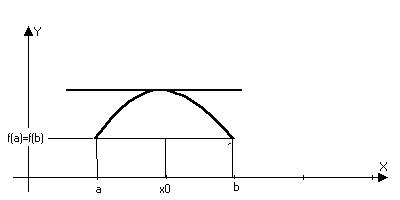
f’(x)=0, то касательная || оси х. Теорема не утверждает, что это единственная точка.

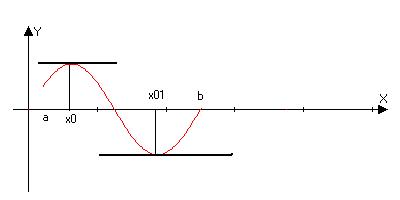
Теорема Лангранджа:

Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (а,b), то $ сÎ(a,b): f(b)-f(a)=f(c)(b-a)

Доказательство:

F(x)=f(x)+lx где l - пока неизвестное число.

F(x) – непрерывна на отрезке [a,b] как сумма непрерывной функции

f(x) – дифференцируема на отрезке [a,b] как сумма дифференцируемой функции.

Выберем число l, так чтобы на отрезке [a,b] F(x) принимало равное значение.

F(a)=f(a)+la

F(b)=f(b)+lb

F(a)=F(b) Þ f(a)-f(b)=l(a-b) Þ l=[f(b)-f(a)]/[b-a]

F(x) – удовлетворяет условию теоремы Роллера на отрезке [a,b] Þ $ cÎ(a,b):F’(c)=0, то есть F’(x)=f’(x)+l

0=f’(c)+l Þ f’(c)=-l=[f(b)-f(a)]/[b-a]

То есть на кривой которая наклонена

к оси х под таким же углом как и секущая

[f(b)-f(a)]/[b-a]=tga=f(x) $ cÎ(a,b)

Замечание:

Часто точку с можно представить в

нужном виде:

с=х₀+q∆х

0<(c-x₀)/(x-x₀)= q<1

c-x₀=q(x-x₀)

c=x₀+q(x-x₀)1

f(x)-f(x₀)=f’(x₀+q∆x)(x-x₀)

0<q<1

∆f(x₀)=f’(x₀+q∆x)∆x

Теорема: (о необходимых и достаточных условиях экстремума по первой производной)

Пусть y=f(x) непрерывна на отрезке [a,b] и дифференцируема в О°(х₀). Если f’(x) меняет знак при переходе через точку х₀, то точка х₀ – точка экстремума. Если меняет знак:

с + на – то это точка максимума

с – на + то это точка минимума

Доказательство: " х₁ Î О°^-(х₀) на [x₁,x₀]; $ c₁Î(x₁,x₀) f(x₀)-f(x₁)=f’(c₁)(x₀-x₁) Þ f(x₀)>f(x₁) "x₁ÎO°^-(x₀)

" х₂ Î О°⁺(х₀) на [x₀,x₂]; $ c₂Î(x₀,x₂) f(x₂)-f(x₀)=f’(c₂)(x₂-x₀) Þ f(x₂)<f(x₀) "x₂ÎO°⁺(x₀)

f(x₀)>f(x) "xÎO°(x₀) Þ точка х точка максимума.

Если в точке х₀ существует производная то она обязательно равна 0 в силе теоремы Ферма. Но могут быть точки в которых f(x) существует, а f’(x) не существует.

Принцип решения подобных задач:

Условие: найти наибольшее и наименьшее значение функции не отрезке [a,b].

Ход решения:

1) Находим точки в которых производная либо равна 0 либо не существует f’(x)=0 или f’(x) $ x₁, x_n

2) Вычисляем знак функции на концах отрезка и в этих точках f(a), f(b), f(x₁)….f(x_n)

3) Выбираем наибольшее и наименьшее m£f(x)<M

Определение: точки в которых функция определена, а производная либо равняется нулю, либо не существует называют критическими точками.