Анализ возмущений сингулярных векторов матриц (блоков матриц) цифровых изображений при разных возмущающих воздействиях
Нормированный вектор является чувствительным (или плохо обусловленным), если малое возмущающее воздействие способно привести к значительному отклонению этого вектора от начального положения, и нечувствительным в противном случае.
Чувствительность СНВ любой матрицы, в том числе и матрицы блока ЦИ, характеризующая величину «ответа» вектора на возмущающее воздействие, различна, в отличие от чувствительности СНЧ (определяемой (8.1)), и в соответствии с соотношением:
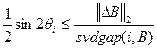 при условии
при условии 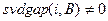 , (8.2)
, (8.2)
где 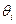 — угол между соответствующими исходным и возмущенным СНВ
— угол между соответствующими исходным и возмущенным СНВ 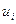 и
и 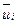 , мерой этой чувствительности является отделенность соответствующего сингулярному вектору сингулярного числа. СНВ, которые отвечают СНЧ с малой отделенностью, являются настолько чувствительными к любым возмущающим воздействиям, что качественно их возмущения не содержат практически никакой информации о реальной величине возмущающего воздействия, а главное, такие СНВ не имеет смысла задействовать в процессе стеганопреобразования: если процесс СП будет формализован совокупностью возмущений таких векторов, то полученное стеганосообщение окажется чувствительным к любому возмущающему воздействию, в частности, к сжатию. Таким образом, полезными с точки зрения анализа и организации процесса СП являются СНВ, СНЧ которых имеют значительную отделенность. Эти векторы малочувствительны не только к сжатию, но и к любому возмущающему воздействию, что будет использовано ниже.
, мерой этой чувствительности является отделенность соответствующего сингулярному вектору сингулярного числа. СНВ, которые отвечают СНЧ с малой отделенностью, являются настолько чувствительными к любым возмущающим воздействиям, что качественно их возмущения не содержат практически никакой информации о реальной величине возмущающего воздействия, а главное, такие СНВ не имеет смысла задействовать в процессе стеганопреобразования: если процесс СП будет формализован совокупностью возмущений таких векторов, то полученное стеганосообщение окажется чувствительным к любому возмущающему воздействию, в частности, к сжатию. Таким образом, полезными с точки зрения анализа и организации процесса СП являются СНВ, СНЧ которых имеют значительную отделенность. Эти векторы малочувствительны не только к сжатию, но и к любому возмущающему воздействию, что будет использовано ниже.
Выясним детально, какие СНВ блоков матрицы ЦИ являются гарантировано малочувствительными к сжатию.
Сингулярные числа блоков, как правило, таковы, что максимальное СНЧ 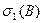 значительно отличается от всех последующих, тем самым имея максимальную отделенность, причем эта отделенность значительно превосходит отделенности всех остальных сингулярных чисел. Это свойство является чрезвычайно значимым в силу следующего. Если отделенность
значительно отличается от всех последующих, тем самым имея максимальную отделенность, причем эта отделенность значительно превосходит отделенности всех остальных сингулярных чисел. Это свойство является чрезвычайно значимым в силу следующего. Если отделенность 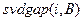 не превосходит
не превосходит 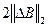 , то (8.2) превращается в тривиальную оценку:
, то (8.2) превращается в тривиальную оценку:
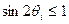 ,
,
которая не дает никакой полезной информации: поведение соответствующих сингулярных векторов непредсказуемо. Эта непредсказуемость объективна и не связана с тем, что для анализа их поведения соотношения (8.2) недостаточно. Для иллюстрации приведем пример. Пусть исходная  и возмущенная
и возмущенная 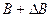 матрицы – это
матрицы – это

При этом 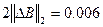 , а отделенности СНЧ принимают значения от 0.001 до 0.004, т.е.
, а отделенности СНЧ принимают значения от 0.001 до 0.004, т.е.
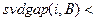
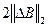 .
.
Это привело к тому, что любой ненулевой вектор длины 8 является СНВ для 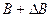 , нет никакой принципиальной возможности оценить возмущение СНВ – угол
, нет никакой принципиальной возможности оценить возмущение СНВ – угол 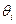 .
.
Будем говорить, что сингулярное число 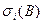 блока
блока  имеет достаточную (недостаточную) отделенность по отношению к возмущению
имеет достаточную (недостаточную) отделенность по отношению к возмущению 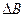 , если
, если
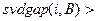
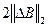 (
( 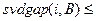
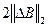 ).
).
Из вышесказанного вытекает важность оценки возможного возмущения блока изображения при сжатии. Понятно, что при снижении коэффициента качества величина возмущающего воздействия при сжатии изображения возрастает. Так, например, при сжатии с 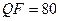 чаще всего блок ЦИ претерпевает возмущение, спектральная норма матрицы которого порядка 10. Это значит, что если отделенность СНЧ блока будет не больше 20, то о поведении соответствующего СНВ в большинстве случаев ничего определенного априори сказать нельзя (такие сингулярные числа будут иметь недостаточную отделенность по отношению к сжатию с
чаще всего блок ЦИ претерпевает возмущение, спектральная норма матрицы которого порядка 10. Это значит, что если отделенность СНЧ блока будет не больше 20, то о поведении соответствующего СНВ в большинстве случаев ничего определенного априори сказать нельзя (такие сингулярные числа будут иметь недостаточную отделенность по отношению к сжатию с 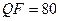 ). При уменьшении коэффициента качества
). При уменьшении коэффициента качества 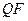 до 60 получается, что достаточная отделенность СНЧ по отношению к такому сжатию должна превосходить 40.
до 60 получается, что достаточная отделенность СНЧ по отношению к такому сжатию должна превосходить 40.
Как показывает вычислительный эксперимент, отделенность максимального СНЧ блоков исходного ЦИ, хранимого без потерь, в подавляющем большинстве случаев будет значительно больше максимального значения нормы матрицы возмущения блока при сжатии, тогда в соответствии с оценкой (8.2), соответствующий такому СНЧ СНВ будет малочувствительным к сжатию (даже при малых 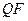 ), причем такой вектор в блоке единственный. Отделенность остальных СНЧ блоков в общем случае не может гарантировать нечувствительности к сжатию своим СНВ даже при большом значении
), причем такой вектор в блоке единственный. Отделенность остальных СНЧ блоков в общем случае не может гарантировать нечувствительности к сжатию своим СНВ даже при большом значении 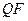 .
.
Поскольку наименее чувствительным к сжатию является СНВ блока, отвечающий максимальному СНЧ, необходимо оценить эту чувствительность количественно. Для этого в среде MATLAB был проведен вычислительный эксперимент, в котором участвовало 200 ЦИ, хранимых без потерь. В ходе эксперимента эти изображения пересохранялись в JPEG с различными коэффициентами качества. Пусть
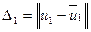 ,
,
где  — СНВ
— СНВ  , отвечающий
, отвечающий 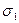 , а
, а 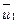 — результат возмущения
— результат возмущения  в процессе сжатия. Результаты эксперимента для 10 выбранных случайно изображений представлены в таблице 8.1, где соответствующие значения получались как среднее арифметическое для
в процессе сжатия. Результаты эксперимента для 10 выбранных случайно изображений представлены в таблице 8.1, где соответствующие значения получались как среднее арифметическое для 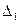 по всем блокам тестируемого изображения. В последней строке таблицы 8.1 даны средние значения
по всем блокам тестируемого изображения. В последней строке таблицы 8.1 даны средние значения 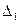 по всем тестируемым 200 ЦИ, в скобках приведены средние значения угла поворота
по всем тестируемым 200 ЦИ, в скобках приведены средние значения угла поворота  при соответствующих сжатиях. Заметим, что
при соответствующих сжатиях. Заметим, что  практически нечувствителен к сжатию даже при сравнительно малом коэффициенте качества
практически нечувствителен к сжатию даже при сравнительно малом коэффициенте качества 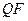 (
( 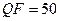 ) в отличие от
) в отличие от 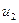 — СНВ блока, отвечающего СНЧ
— СНВ блока, отвечающего СНЧ 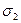 , который оказывается заметно чувствительным к сжатию даже с большим коэффициентом качества
, который оказывается заметно чувствительным к сжатию даже с большим коэффициентом качества 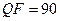 (табл.8.2 (здесь
(табл.8.2 (здесь 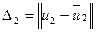 , где
, где 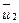 — результат возмущения
— результат возмущения 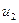 в процессе сжатия). Для СНВ, отвечающих
в процессе сжатия). Для СНВ, отвечающих 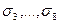 , качественная картина их чувствительности, как следует из всего вышесказанного, будет еще хуже, чем для
, качественная картина их чувствительности, как следует из всего вышесказанного, будет еще хуже, чем для 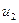 .
.
Таблица 8.1
Среднее значение 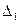 по TIF-изображению при сжатии с различным коэффициентом качества
по TIF-изображению при сжатии с различным коэффициентом качества 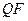
Знач-е 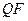 № ЦИ
№ ЦИ
|
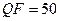
|
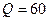
|
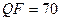
|
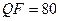
|
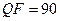
|
| 0.0116 | 0.0083 | 0.0063 | 0.0043 | 0.0029 | |
| 0.1500 | 0.1030 | 0.0810 | 0.0616 | 0.0455 | |
| 0.0077 | 0.0051 | 0.0038 | 0.0026 | 0.0017 | |
| 0.0133 | 0.0082 | 0.0059 | 0.0040 | 0.0025 | |
| 0.0086 | 0.0062 | 0.0048 | 0.0032 | 0.0021 | |
| 0.0074 | 0.0060 | 0.0049 | 0.0037 | 0.0022 | |
| 0.0117 | 0.0084 | 0.0065 | 0.0046 | 0.0026 | |
| 0.0145 | 0.0092 | 0.0067 | 0.0046 | 0.0028 | |
| 0.0130 | 0.0095 | 0.0076 | 0.0055 | 0.0037 | |
| 0.0126 | 0.0089 | 0.0068 | 0.0048 | 0.0032 | |
Среднее значение 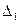 (200 ЦИ) (200 ЦИ)
| 0.0251 (1.4o) | 0.0194 (1.1o) | 0.0156 (0.89o) | 0.0115 (0.66o) | 0.0078 (0.45o) |
Таким образом, очевиден вывод: для того, чтобы стеганографический алгоритм был устойчивым к сжатию, достаточно производить стеганопреобразование так, чтобы его формальным представлением была совокупность возмущений сингулярных векторов блоков ЦИ-контейнера, отвечающих максимальным СНЧ (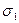 ) этих блоков.
) этих блоков.
Процесс стеганопреобразования должен строиться таким образом, чтобы для стеганосообщения обеспечивалась надежность восприятия. В силу этого необходимо получить, в первую очередь, качественные оценки возможного возмущения  при организации процесса погружения дополнительной информации.
при организации процесса погружения дополнительной информации.
Таблица 8.2
Среднее значение 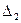 по TIF-изображению при сжатии с различным коэффициентом качества
по TIF-изображению при сжатии с различным коэффициентом качества 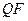
Знач-е 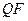 № ЦИ
№ ЦИ
|
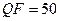
|
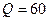
|
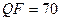
|
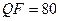
|
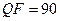
|
| 0.9955 | 0.8044 | 0.6843 | 0.5206 | 0.3805 | |
| 0.7658 | 0.5602 | 0.4505 | 0.3263 | 0.2193 | |
| 0.7130 | 0.5552 | 0.4694 | 0.3635 | 0.2545 | |
| 0.3571 | 0.2484 | 0.2005 | 0.1538 | 0.1042 | |
| 0.9641 | 0.7881 | 0.6743 | 0.5239 | 0.3272 | |
| 0.9319 | 0.8063 | 0.7456 | 0.6738 | 0.5470 | |
| 0.8925 | 0.6961 | 0.6350 | 0.5999 | 0.4103 | |
| 0.4395 | 0.3160 | 0.2541 | 0.1856 | 0.1161 | |
| 0.8594 | 0.7338 | 0.6680 | 0.5567 | 0.3856 | |
| 0.8257 | 0.6630 | 0.5643 | 0.4321 | 0.2935 | |
Среднее значение 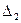 (200 ЦИ) (200 ЦИ)
| 0.7721 (45.42o) | 0.6210 (36.18o) | 0.5420 (31.45o) | 0.4441 (25.66o) | 0.3129 (18.00o) |
Как вытекает из неравенства (8.2), возмущение  не может быть значительным. Действительно, поскольку (8.2) имеет место для каждого СНВ матрицы
не может быть значительным. Действительно, поскольку (8.2) имеет место для каждого СНВ матрицы  , то из него получаем:
, то из него получаем:
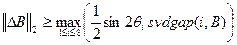 , (8.3)
, (8.3)
откуда вытекает, что при значительной отделенности 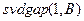 максимального сингулярного числа даже небольшое возмущение
максимального сингулярного числа даже небольшое возмущение  , которое выражается в повороте этого вектора на угол
, которое выражается в повороте этого вектора на угол 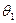 , может привести к значительному возмущению матрицы блока, что, в свою очередь, с большой вероятностью повлечет за собой нарушение надежности восприятия изображения-стеганосообщения.
, может привести к значительному возмущению матрицы блока, что, в свою очередь, с большой вероятностью повлечет за собой нарушение надежности восприятия изображения-стеганосообщения.
Характер поведения вектора  определяются не только соотношением (8.3). По теореме Фробениуса любая неразложимая неотрицательная матрица
определяются не только соотношением (8.3). По теореме Фробениуса любая неразложимая неотрицательная матрица 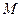 всегда имеет положительное собственное значение
всегда имеет положительное собственное значение 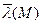 , являющееся простым корнем соответствующего ей характеристического уравнения. Модули всех других собственных значений не превосходят
, являющееся простым корнем соответствующего ей характеристического уравнения. Модули всех других собственных значений не превосходят 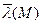 . Собственному значению
. Собственному значению 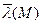 соответствует собственный вектор
соответствует собственный вектор 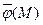 с положительными координатами.
с положительными координатами.
Для блока контейнера с матрицей  матрица
матрица 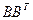 является симметричной:
является симметричной:
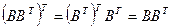 ,
,
для которой с учетом нормального сингулярного разложения для 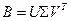 имеет место соотношение:
имеет место соотношение:
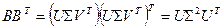 , (8.4)
, (8.4)
которое в силу ортогональности матрицы 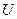 и лексикографической положительности ее столбцов, а также диагональности матрицы
и лексикографической положительности ее столбцов, а также диагональности матрицы
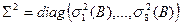 (8.5)
(8.5)
представляет собой нормальное спектральное разложение 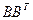 , определяемое однозначно. При этом столбцы матрицы
, определяемое однозначно. При этом столбцы матрицы 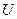 — собственные векторы
— собственные векторы 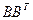 , а диагональные элементы матрицы
, а диагональные элементы матрицы 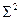 — собственные значения
— собственные значения 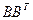 (все они неотрицательные, как следует из (8.5)). По теореме Фробениуса максимальному собственному значению
(все они неотрицательные, как следует из (8.5)). По теореме Фробениуса максимальному собственному значению
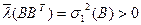 (8.6)
(8.6)
отвечает собственный вектор 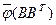 (первый столбец матрицы
(первый столбец матрицы 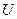 ) с положительными координатами, но этот собственный вектор одновременно является левым сингулярным вектором
) с положительными координатами, но этот собственный вектор одновременно является левым сингулярным вектором  блока
блока  , отвечающим максимальному СНЧ
, отвечающим максимальному СНЧ 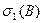 . Аналогичное утверждение будет следовать для правого СНВ
. Аналогичное утверждение будет следовать для правого СНВ  блока
блока  , отвечающего
, отвечающего 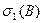 :
:  имеет все положительные координаты, поскольку для симметричной матрицы
имеет все положительные координаты, поскольку для симметричной матрицы 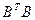 (
( 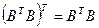 ) имеет место равенство, аналогичное (8.4):
) имеет место равенство, аналогичное (8.4):
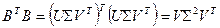 .
.
Таким образом, в любой неразложимой неотрицательной матрице  блока ЦИ левый и правый СНВ, отвечающие максимальному СНЧ, имеют положительные координаты. Необходимо отметить, что левый (правый) сингулярный вектор, все компоненты которого положительны, единственный для
блока ЦИ левый и правый СНВ, отвечающие максимальному СНЧ, имеют положительные координаты. Необходимо отметить, что левый (правый) сингулярный вектор, все компоненты которого положительны, единственный для  при ортонормированности СНВ.
при ортонормированности СНВ.
Важно, что независимо от силы возмущающего воздействия, которое претерпевает цифровое изображение, его матрица (матрицы его блоков) остаются неразложимыми неотрицательными, а значит и обсуждаемые СНВ будут после возмущения (даже сильного) иметь все положительные координаты, поэтому эти векторы является не только устойчивыми, но и sign-устойчивыми к любому возмущающему воздействию.
Вектор является sign-неустойчивым, если даже малые возмущающие воздействия могут привести к изменению знаков его координат, и sign-устойчивым в противном случае. Наибольшей sign-устойчивостью среди нормированных векторов пространства 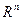 обладает так называемый n-оптимальный вектор:
обладает так называемый n-оптимальный вектор:
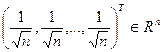 ,
,
образующий равные углы со всеми координатными плоскостями 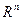 .
.
Особенностью sign-устойчивости левого и правого сингулярных векторов, отвечающих максимальному сингулярному числу матрицы блока цифрового изображения является то, что она имеет место не только при малых возмущающих воздействиях, но и при воздействиях любой силы, в том числе, при сжатии изображения со значительными коэффициентами, причем это свойство присуще упомянутым векторам как до, так и после произвольного возмущающего воздействия (оставляющего блоки неразложимыми), которому подвергается изображение. Очевидно, что если стеганопреобразование будет организовано таким образом, что его формальным представлением будет совокупность возмущений СНВ  и
и  блоков матрицы контейнера, то сжатие СС, в том числе, со значительными коэффициентами, не затронет или затронет незначительно погруженную информацию, обеспечивая устойчивость соответствующего стеганоалгоритма к атаке сжатием.
блоков матрицы контейнера, то сжатие СС, в том числе, со значительными коэффициентами, не затронет или затронет незначительно погруженную информацию, обеспечивая устойчивость соответствующего стеганоалгоритма к атаке сжатием.
Все вышесказанное приводит к следующему качественному выводу относительно взаимного расположения векторов  ,
,  и n-оптимального.
и n-оптимального.
Утверждение. СНВ 8*8-блоков матрицы ЦИ (  ,
,  ), отвечающие наибольшим СНЧ (
), отвечающие наибольшим СНЧ ( 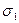 ), близки к n-оптимальному вектору пространства
), близки к n-оптимальному вектору пространства 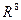 независимо от величины и вида возмущающего воздействия, которое претерпевает цифровое изображение, от формата его хранения, т.е. углы между векторами
независимо от величины и вида возмущающего воздействия, которое претерпевает цифровое изображение, от формата его хранения, т.е. углы между векторами  и n-оптимальным,
и n-оптимальным,  и n-оптимальным, а потому и между
и n-оптимальным, а потому и между  и
и  для подавляющего большинства блоков изображения имеют малые значения.
для подавляющего большинства блоков изображения имеют малые значения.
Проведенный вычислительный эксперимент с учетом того, что в пространстве 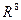 n-оптимальный вектор имеет следующий вид:
n-оптимальный вектор имеет следующий вид:
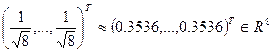 ,
,
подтверждает полученное теоретическое заключение. Иллюстрацией этому является левый, правый сингулярные векторы, отвечающие максимальному сингулярному числу одного случайно выбранного блока случайно выбранных цифровых изображений, приведенные в таблице 8.3. Изображения брались различными для каждого примера таблицы 8.3.
Таблица 8.3
Дата добавления: 2016-07-22; просмотров: 2420;











