Узагальнені координати і узагальнені сили
Узагальненими координатами системи називаються незалежні одна від одної величини q1, q2,…,qs, які повністю і однозначно визначають положення системи в довільно вибраний момент часу.
Узагальнені координати мають розмірність довжини, кута і т. ін.
Узагальнена швидкість - це перша похідна від узагальненої координати за часом:
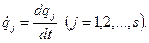 (17.24)
(17.24)
Кожній узагальненій координаті відповідає своя узагальнена швидкість.
Число незалежних узагальнених координат qj механічної системи з ідеальними голономними в’язями дорівнює числу ступенів вільності.
Швидкість k-тої матеріальної точки дорівнює:
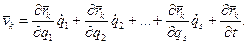 (17.25)
(17.25)
Узагальнені сили можна обчислити такими методами:
а) методом визначення коефіцієнтів в формулі суми елементарних робот активних сил при відповідних узагальнених можливих переміщеннях. В цьому випадку треба:
1) визначити число ступенів вільності даної системи і вибрати відповідні узагальнені координати;
2) показати всі активні сили, діючі на систему;
3) якщо не всі в’язі, накладені на матеріальну систему, є ідеальними, то включити до активних сил відповідні реакції в’язей;
4) надати системі незалежні узагальнені можливі переміщення;
5) для визначення узагальненої сили Qj, відповідної до j-тої узагальненої координати qj, треба обчислити суму робот всіх активних сил на узагальненому можливому переміщенні δqj. При цьому решта узагальнених можливих переміщень δq1=δq2=…=δqj-1=δqj+1=…=δqs=0. Узагальнена сила Qj буде дорівнювати коефіцієнту при δqj. Аналогічно обчислюють й інші узагальнені сили;
б) методом визначення узагальнених сил через потенціальну енергію системи.
Якщо всі сили, що діють на механічну систему, потенціальні, то треба:
1) визначити узагальнені координати;
2) обчислити потенціальну енергію П системи
П=П(q1, q2,…,qs);
3) визначити узагальнену силу за формулою
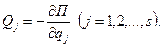
Дата добавления: 2016-07-18; просмотров: 2948;











