Принцип можливих переміщень

Розглянемо голономну механічну систему зі стаціонарними в’язями. Для такої системи справедливий принцип: для рівноваги в даному положенні механічної системи з ідеальними в’язями необхідно і достатньо, щоб сума можливих робот всіх активних сил на будь-якому можливому переміщенні системи з даного положення дорівнювала нулю:

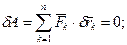(17.23)

в проекціях на осі декартових координат

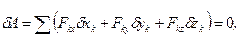
де F_kx, F_ky, F_kz - проекції рівнодійної активних сил, які діють на k-ту матеріальну точку; δx_k, δy_k, δz_k – проекції можливого переміщення k-тої точки.

Розв’язувати задачі на рівновагу твердих тіл і систем твердих тіл за допомогою принципу можливих переміщень рекомендується в такому порядку:

1) показати на рисунку активні сили;

2) при наявності неідеальних в’язей додати відповідні реакції в’язей (наприклад, сили тертя);

3) у випадку, коли треба визначити реакцію в’язі, потрібно відкинути відповідну в’язь і замінити її шуканою реакцією.

Для систем з одним ступенем вільності:

4) дати можливе переміщення одній точці системи і виразити можливі переміщення точок прикладання сил в залежності від даного переміщення;

5) обчислити роботу всіх сил на відповідних можливих переміщеннях і прирівняти цю суму до нуля;

6) розв’язати складене рівняння рівноваги, визначити шукану величину.

Для систем з декількома ступенями вільності:

4) вибрати незалежні можливі переміщення точок системи, їх число повинно дорівнювати числу ступенів вільності цієї системи;

5) дати можливе переміщення, яке відповідає одному ступеню вільності системи, вважаючи при цьому можливі переміщення, які відповідають решті ступенів вільності, рівними нулю. Виразити можливі переміщення точок прикладання сил через дане можливе переміщення;

6) обчислити суму робот всіх сил на відповідних переміщеннях точок їх прикладання і цю суму прирівняти до нуля;

7) послідовно провести викладку пунктів 5 і 6 для кожного з незалежних переміщень і скласти систему рівнянь, число яких дорівнює числу ступенів вільності системи;

8) розв’язати систему рівнянь рівноваги, знайти необхідні величини.