Моменти iнерцiї твердого тiла

Загальнi формули для визначення моментiв iнерцiї твердого тiла. Радiус iнерцiї

Моментом iнерцiї твердого тіла або системи матерiальних точок вiдносно даної точки О, осi L, площини П називається скалярна величина, яка дорiвнює сумi добуткiв мас всiх точок тiла та квадратів їх вiддалей до даної точки О, осi L або площини П вiдповiдно. Позначають: I_O - момент iнерцiї вiдносно даної точки О, I_L -момент iнерцiї вiдносно осi L, I_П - момент iнерцiї вiдносно площини П:

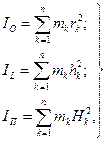(12.1)

де m_k - маса k-тої точки системи, r_k, h_k, H_k - її вiдстанi до даної точки О, осi L i площини П відповідно.

Одиниця вимiрювання моментiв iнерцiї в системi СI

[I] = кг×м².

Якщо механiчна система утворює суцiльне тiло, то в (12.1) суми треба замiнити вiдповiдними iнтегралами. Наприклад, момент iнерцiї суцiльного тiла вiдносно осi обчислимо за формулою:

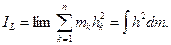(12.2)

У випадку однорiдного твердого тiла

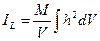, де V – об’єм тiла. (12.3)

Для декартової системи координат (рис. 12.1):

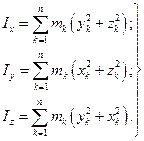(12.4)

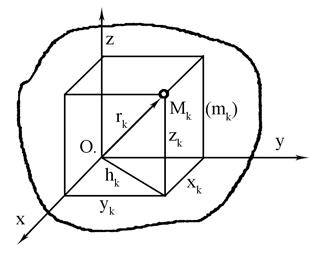
Рис. 12. 1.

Полярний момент iнерцiї (момент iнерцiї вiдносно точки О) дорiвнює:

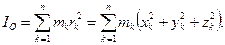(12.5)

Моменти iнерцiї вiдносно координатних площин дорiвнюють:

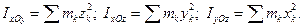(12.6)

В такому разi з формул (12.4) – (12.6) знайдемо:

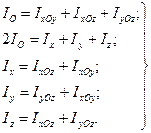(12.7)

Радiус iнерцiї – це вiдстань вiд осi до тiєї точки, в якiй потрiбно зосередити масу всього тiла, щоб момент iнерцiї цiєї точки дорiвнював моменту iнерцiї всього тiла:

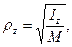(12.8)

тобто, при заданому радiусi iнерцiї r_z момент iнерцiї I_z обчислюють за формулою:

I_z = Mr_z². (12.9)

Теорема Штейнера

Момент iнерцiї твердого тiла вiдносно осi дорiвнює сумi його моменту iнерцiї вiдносно паралельної осi, яка проходить через центр мас С (рис. 12.2) i добутка маси тiла та квадрату вiдстанi мiж паралельними осями, тобто

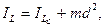(12.10)

де L_С - вiсь, що проходить через центр ваги (центр мас) С, 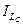- момент iнерцiї тiла вiдносно осi L_С, d - вiдстань мiж осями L i L_С.

Якщо при розв’язуваннi задач необхiдно обчислити момент iнерцiї тiла вiдносно осi, що не проходить через центр ваги твердого тiла, то проводять паралельну вiсь через центр ваги твердого тiла i застосовують теорему Штейнера.

При обчисленнi моментiв iнерцiї твердих тiл задача часто зводиться до обчислення вiдповiдних iнтегралiв.