ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА

План

1. Абсолютное твёрдое тело. Вращательное движение. Угловая скорость и угловое ускорение, их связь с линейными скоростями и ускорениями вращающегося твёрдого тела.

2. Момент инерции тела. Кинетическая энергия вращающегося твёрдого тела.

3. Вычисление моментов инерции. Теорема Штейнера. Свободные оси.

4. Момент силы. Момент импульса.

5. Уравнение моментов. Уравнение динамики вращательного движения твёрдого тела относительно неподвижной оси.

6. Гироскопы. Гироскопический эффект.

1. Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, деформацией которого в условиях данной задачи можно пренебречь. Расстояние между любыми двумя точками тела остаётся неизменным.

Всякое движение твёрдого тела можно разложить на два основных вида движения – поступательное и вращательное.

Вращательнымназывается такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.

Введём понятие угловой скорости и углового ускорения. Пусть твёрдое тело вращается вокруг неподвижной в данной системе отсчёта оси 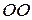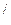и за время 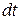совершает бесконечно малый поворот (рис. 3.1).

Соответствующий угол поворота будем характеризовать вектором 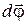, модуль которого равен углу поворота, а направление совпадает с осью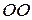 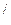, причём так, что направление поворота отвечает правилу правого винта по отношению к направлению вектора .

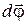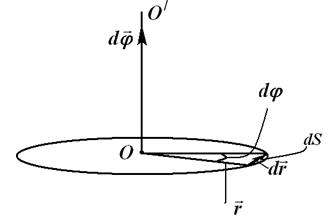
Рис. 3.1

Из рис. 3.1 следует, что 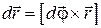. Вектор 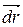как бесконечно малую величину можно считать по модулю равным соответствующей дуге окружности 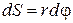, его направление соответствует правилу правого винта по отношению к векторам 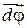и

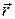
Разделим обе части на :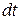

. (*)

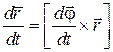Производная угла поворота по времени называется угловой скоростью.

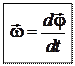
Вектор 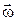совпадает по направлению с вектором 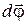. Изменение вектора 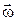со временем характеризуют вектором углового ускорения:

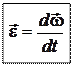
Из выражения * получаем связь линейной 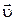и угловой скоростей:

(**)

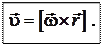То есть скорость 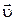любой точки А твёрдого тела, вращающегося вокруг неподвижной оси с угловой скоростью 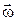, равна векторному произведению 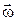на радиус-вектор 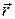точки А относительно произвольной точки на оси вращения.

Если выбрать в качестве точки отсчёта для радиус-вектора центр окружности вращения (точка О), при неизменном радиусе окружности 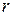выражение (**) можно записать в скалярном виде:

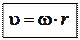
Продифференцируем это выражение по времени: 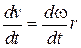, отсюда получаем связь тангенциального и углового ускорений:

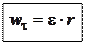
Нормальное ускорение можно представить как

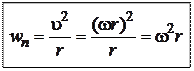
Модуль полного ускорения:

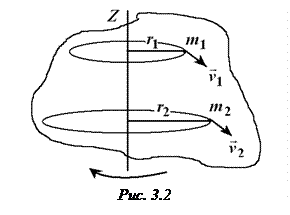2. Момент инерции тела. Определим кинетическую энергию вращения твёрдого тела (рис. 3.2). Разделим его мысленно на отдельные элементарные части, настолько малые, чтобы их можно было считать движущимися как материальные точки ( 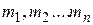). Обозначим массу i-го элемента 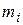, а скорость этого элемента .

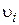Кинетическая энергия этого элемента

.

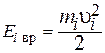Просуммировав кинетическую энергию всех элементов, получим кинетическую энергию вращательного движения тела:

.

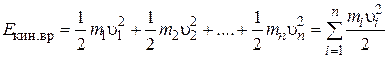Линейная скорость 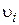связана с угловой скоростью вращения тела 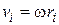( 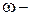постоянна для всех точек тела).

.

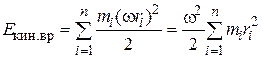Определение. Моментом инерции материальной точки относительно оси z называется произведение массы этой точки на квадрат её расстояния от оси вращения:

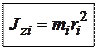
Определение. Моментом инерции твёрдого тела относительно некоторой оси z называется сумма моментов инерций материальных точекотносительно данной оси.

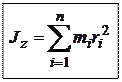
В соответствии с этими определениями:

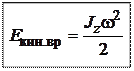
(Сравните с выражением для кинетической энергии поступательного движения 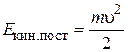, очевидно соответствие ).

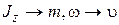Физический смысл момента инерции. Момент инерции во вращательном движении играет такую же роль, как масса при поступательном движении, характеризует меру инертности тела при вращательном движении. Чем больше момент инерции тела, тем труднее при прочих равных условиях привести его во вращательное движение. Момент инерции определяется не только массой, но и тем, как эта масса распределена относительно оси вращения.

Соотношение 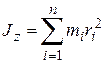является приближённым, причём тем более точным, чем меньше элементарные массы 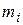. Задача нахождения моментов инерции сводится к интегрированию.

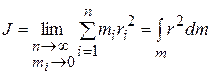
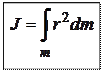
(Интегрирование ведётся по всей массе тела ).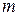

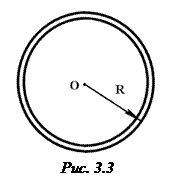3. Вычисление моментов инерции. 1. Кольцо (полый цилиндр) (рис. 3.3). В случае достаточно тонких стенок вся масса сосредоточена на расстоянии 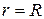от центра.

Относительно оси, проходящей через центр кольца:

,

.

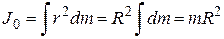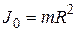2. Однородный диск (сплошной цилиндр)

Дано: 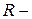радиус диска, 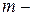масса диска.

Найти: 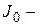момент инерции диска относительно оси, проходящей через центр диска.

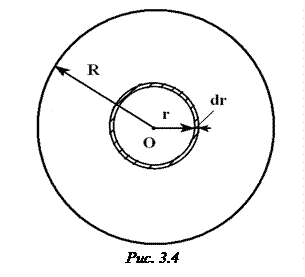
Разобьём диск (рис. 3.4) на кольца с радиусом 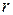, толщиной 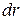. По определению момента инерции 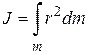. Пусть 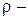поверхностная плотность диска 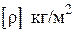, тогда масса кольца 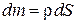, где 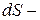площадь кольца, 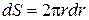. Интегрируя по радиусу, находим момент инерции диска:

= ,

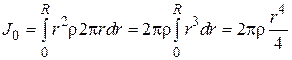
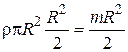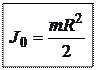
3. Тонкий однородный стержень

Дано: 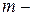масса стержня, 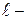длина стержня.

Найти: 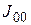(момент инерции относительно оси ОО, проходящей через конец стержня перпендикулярно ему) (рис. 3.5).

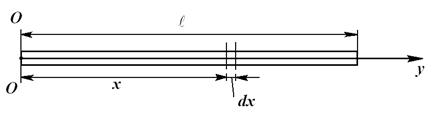
Рис. 3.5

Ввиду одномерного характера задачи выражение 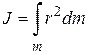можно заменить на 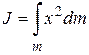, где 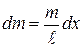, тогда .

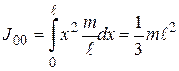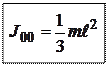
Теорема Штейнера (без вывода)

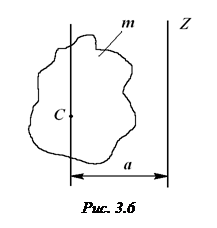Постановка задачи. Известен момент инерции произвольного тела массой 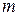относительно оси, проходящей через его центр тяжести 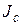(рис. 3.6). Требуется найти, каков момент инерции 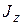относительно какой-либо оси 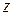, параллельной первой и находящейся на расстоянии 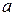от неё.

Теорема. Момент инерции тела относительно произвольной оси z равен сумме момента инерции относительно оси, проходящей через центр масс тела С и параллельной данной, и произведения массы тела на квадрат расстояния между осями a:

.

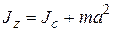Пример применения теоремы Штейнера.

Требуется найти момент инерции тонкого однородного стержня массой 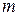и длиной 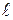относительно перпендикулярной к нему оси 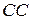, проходящей через центр стержня (рис. 3.7).

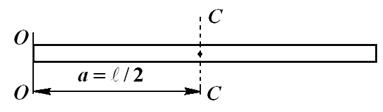
Рис. 3.7

Решение:

Воспользуемся полученным ранее выражением для момента инерции стержня относительно оси, проходящей через его конец:

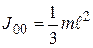. Используя теорему Штейнера, получаем:

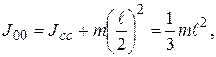отсюда .

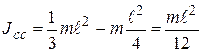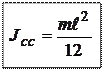
Свободные оси

Определение. Ось вращения тела, положение которой в пространстве остаётся неизменным без действия на неё внешних сил, называется свободной.

Можно доказать, что в любом теле существует три взаимно перпендикулярных оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называются главными осями инерции тела. Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней. Вращение вокруг главных осей с наибольшим и наименьшим (экстремальными) моментами инерции оказывается устойчивым, а вращение вокруг оси со средним моментом – неустойчивым. Этот факт является достаточно важным при проектировании конструкций с вращающимися частями.

4. Момент силы. Пусть О – какая-либо точка, относительно которой рассматривается момент вектора силы. Обозначим 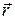радиус-вектор, проведённый из этой точки к точке приложения силы 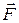(Рис. 3.8).

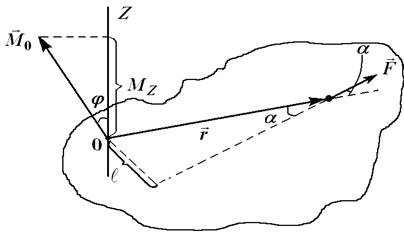
Рис. 3.8

Определение. Моментом силы 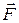относительно точки О называется векторное произведение радиуса-вектора 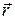на силу :

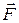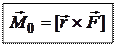
Раскрывая векторное произведение, получим 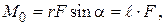где 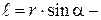плечо силы (длина перпендикуляра, опущенного из точки О на линию действия силы).

В соответствии с определением векторного произведения вектор 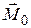направлен перпендикулярно плоскости, в которой лежат векторы 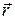и 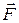в соответствии с правилом правого винта (буравчика).

Определение. Момент силы относительно оси 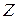, проходящей через точку О, есть проекция на эту ось вектора момента силы 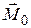относительно точки, лежащей на этой же оси.

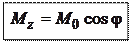
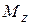как проекция на ось является скалярной величиной.

Момент импульса

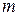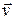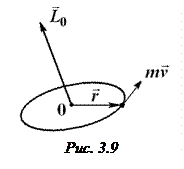
Пусть материальная точка массой движется со скоростью относительно точки О, а 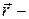радиус-вектор этой материальной точки, проведённый из точки О (рис. 3.9).

Определение. Моментом импульса материальной точки относительно точки О называется векторное произведение радиуса-вектора 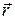на вектор импульса :

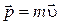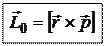
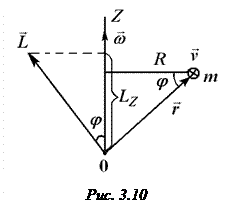Направление 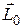перпендикулярно плоскости, в которой лежат векторы 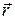и 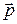, в соответствии с правилом правого винта, например момент импульса электрона, двигающегося по круговой орбите в боровской модели атома.

Свяжем момент импульса с моментом инерции и угловой скоростью. Пусть радиус-вектор 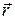некоторой частицы массой 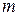лежит в плоскости рис. 3.10, скорость 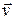перпендикулярна ей («от нас»), частица движется по окружности радиусом .

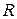Модуль момента импульса 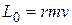. Линейную скорость 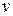можно связать с угловой 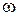относительно оси 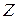как 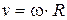, тогда 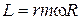. Проекция вектора 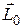на ось вращения равна

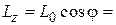
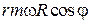. Как видно из рис. 3.10, 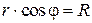, т.е.

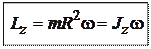
Для системы материальных точек (твёрдого тела) выражение связ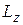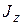и , и 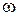формально такое, как и для материальной точки:

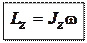
Но под 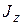здесь подразумевается сумма моментов инерции материальных точек системы:

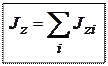
Можно показать (см., например, в [1]), что для однородного тела, симметричного относительно оси вращения, суммарный момент импульса тела 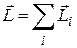. Он направлен вдоль оси вращения в ту же сторону, что и 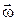, т.е.

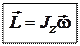
(Для несимметричного тела в общем случае 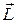не совпадает по направлению с вектором ).

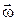5. Уравнение моментов. В дальнейших преобразованиях условимся для упрощения записи индекс 0 у 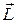, 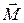и других величин не писать, но подразумевать, что он есть.

Продифференцируем выражение для момента импульса материальной точки: . .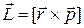

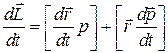Учтём, что 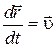, а .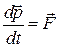

Рассмотрим первое слагаемое (см. в лекции № 1 «Векторное произведение»).

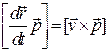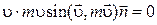= (так как угол между 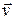и 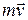равен нулю).

Второе слагаемое в выражении для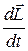

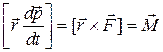(по определению момента силы).

В результате получаем:

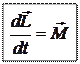Уравнение моментов (оно связывает момент импульса с моментом силы).

Производная по времени момента импульса материальной точки относительно точки О равна моменту действующей силы относительно точки О.