Моменти iнерцiї тiла вiдносно осей, якi проходять через задану точку

Момент iнерцiї тiла вiдносно осi L (рис. 12.3) обчислюють за формулою:

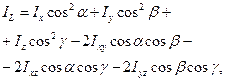(12.11)

де I_х, I_у, I_z - осьовi моменти iнерцiї тiла; I_хy, I_уz, I_xz - вiдцентровi моменти iнерцiї вiдносно осей х, у, z:

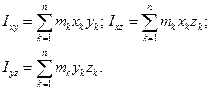(12.12)

Геометричне мiсце кiнцiв вiдрiзкiв

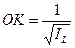(12.13)

розмiститься на поверхнi, яка називається елiпсоїдом iнерцiї.

Для кожної точки О тiла маємо свiй елiпсоїд iнерцiї. Елiпсоїд iнерцiї центра мас тiла називається центральним елiпсоїдом iнерцiї. Осi елiпсоїда iнерцiї називаються головними осями iнерцiї. В загальному випадку елiпсоїд iнерцiї має три взаємо перпендикулярнi головнi осi iнерцiї. Вони є його осями симетрiї.

Моменти iнерцiї вiдносно головних осей iнерцiї називаються головними моментами iнерцiї, а вiдносно головних центральних осей iнерцiї - головними центральними моментами iнерцiї.

В загальному випадку рiвняння елiпсоїда iнерцiї має вигляд:

I_x x² + I_yy² + I_zz² - 2I_xyxy - 2I_xzxz - 2I_yzyz = l. (12.14)

Якщо це рiвняння елiпсоїда iнерцiї вiднести до його головних осей Оx₁, Оу₁, Оz₁, то воно приймає вигляд

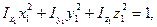(12.15)

де x₁, у₁, z₁ - координати точки, розташованої на елiпсоїдi iнерцiї, вiдносно головних осей iнерцiї; 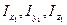- головнi моменти iнерцiї.

Вiдцентровi моменти iнерцiї вiдносно головних осей iнерцiї дорiвнюють нулю, тобто

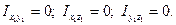(12.16)

Правильним є i зворотне ствердження: якщо вiдцентровi моменти iнерцiї вiдносно трьох взаємно перпендикулярних осей дорiвнюють нулю, то цi осi є головними осями iнерцiї.

Головнi моменти iнерцiї часто позначають I₁, I₂, I₃ замiсть 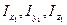. Тодi для головних осей iнерцiї формула (12.11) набуває вигляду

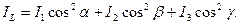(12.17)

Розглянемо властивостi головних осей інерції.

1. Щоб вiсь Оx була головною вiссю iнерцiї тiла для початку координат, необхiдно i достатньо, щоб дорiвнювали нулю вiдцентровi моменти iнерцiї, якi мiстять iндекс х:

I_xy = 0; I_xz = 0.

2. Якщо тiло має форму нескiнченної тонкої пластинки, то одна з головних осей iнерцiї для кожної точки тiла перпендикулярна до площини пластинки.

3. Якщо однорiдне тiло має площину симетрiї, то в кожнiй точцi цiєї площини одна з головних осей iнерцiї перпендикулярна до площини симетрiї.

4. Кожна головна центральна вiсь iнерцiї залишається головною вiссю для всiх своїх точок, а двi iншi головнi осi зберiгають паралельнiсть вiдповiдним головним центральним осям інерції.

5. Якщо однорiдне тiло має двi взаємно перпендикулярнi площини симетрiї, то лiнiя їх перетину є однiєю з головних центральних осей iнерцiї.