Теорема про змiну кiнетичної енергiї матерiальної точки. Потенцiальнi силовi поля. Закон збереження механiчної енергiї точки

Теорема про змiну кiнетичної енергiї точки. Прирiст кiнетичної енергiї рухомої матерiальної точки на нескiнченно малому її перемiщеннi дорiвнює елементарнiй роботi прикладеної сили на тому ж перемiщеннi:

dT = d(mv²/2) = 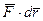= δA, (9.29)

де m - маса матерiальної точки, v - її швидкість, dr = vdt - елементарне перемiщення точки за проміжок часу dt, Т - кiнетична енергія точки.

Якщо проiнтегрувати рiвняння (9.29) вiд початкового положення точки до кiнцевого, то одержимо

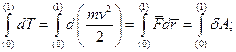
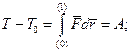
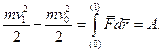(9.30)

З рiвняння (9.30) випливає теорема: прирiст кiнетичної енергiї рухомої матерiальної точки дорiвнює роботi прикладеної сили на даному вiдрiзку шляху.

Силовi поля. Закон збереження механiчної енергiї матерiальної точки.

Частина простору, в кожнiй точцi якого на матерiальну точку дiє певна сила, що є однозначною функцiєю координат точки i, можливо, часу, але не залежить вiд швидкостi руху точки, називається силовим полем.

Силове поле, сили якого не залежать вiд часу, називається стацiонарним.

Стацiонарне силове поле, в якому робота сили поля, прикладеної до матерiальної точки, що рухається в ньому, залежить вiд початкового i кiнцевого положень цiєї точки, а значить, не залежить вiд шляху, по якому перемiщується точка в просторi, називається потенцiальним.

Прикладами потенцiальних силових полiв є: поле тяжiння, електростатичне поле, поле пружних сил.

Потенцiальна енергiя в даному положеннi матерiальної точки визначається роботою сили поля на перемiщеннi точки iз заданого її положення в певне фiксоване:

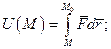
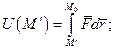
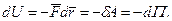(9.31)

Отже, елементарна робота, виконувана силою потенцiального силового поля, дорiвнює повному диференцiалу потенцiальної енергiї, взятому зi знаком ”мінус”.

При русi матерiальної точки в потенцiальному силовому полi повна механiчна енергiя точки зберiгає сталу величину:

dT = δA = - dU;

(mv²/2) + U(x, y, z) = H. (9.32)

Суму кiнетичної та потенцiальної енергiй називають повною механiчною енергiєю точки.

При розв’язуваннi задач на застосування теореми про змiну кiнетичної енергiї матерiальної точки доцiльно дотримуватися такого порядку:

1) вибрати об’єкт дослiдження, прийняти його за матерiальну точку i показати її в довiльний момент часу;

2) прикласти активнi (заданi) сили;

3) вiдкинути в’язi, замiнивши їх реакцiями;

4) застосувати теорему про змiну кiнетичної енергiї для деякого вiдрiзку шляху;

5) виразити кiнетичну енергiю в початковий i кiнцевий моменти часу i роботу всiх сил, прикладених до точки, через заданi i шуканi величини;

6) розв’язати одержане рiвняння.

Зауваження. Для закріплення матеріалу §9 (пункти 9.2 і 9.3) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 29.1, 29.2, 29.6, 29.7, 30.3, 30.4, 30.14;

2) № 29.9, 29.10, 29.11, 29.12, 29.14, 30.6, 30.7, 30.9, 30.10, 30.11, 30.13, 30.15, 30.16, 30.17, 30.21, 30.25, 30.50;

3) № 29.15, 29.16, 30.18, 30.19, 30.20, 30.22, 30.27, 30.28, 30.29, 30.30, 32.51, 32.52.

Питання для самоконтролю

1. Сформулюйте поняття роботи сили.

2. Як визначається робота постійної за модулем і напрямом сили на прямолінійному переміщенні? Чим визначається знак такої роботи?

3. Запишіть три випадки визначення роботи сталої сили при різних кутах між напрямами сили і переміщення.

4. Яку роботу сили називають елементарною?

5. Назвіть і поясніть фізичну суть одиниці вимірювання роботи в системі СІ.

6. Сформулюйте теорему про елементарну роботу рівнодійної.

7. Як визначається елементарна робота сили через проекції сили на осі декартових координат?

8. Як визначити роботу змінної сили на скінченному переміщенні по криволінійній траєкторії?

9. Запишіть формулу визначення роботи змінної сили на скінченному переміщенні по криволінійній траєкторії через проекції сили на осі декартових координат.

10. Як визначається робота сили ваги матеріальної точки?

11. Чи залежить робота сили тяжіння від форми траєкторії матеріальної точки?

12. Сформулюйте правило знаків при визначенні роботи сили ваги.

13. В якому випадку робота сили ваги дорівнює нулю?

14. Як визначається робота сили всесвітнього тяжіння?

15. Сформулюйте і запишіть, як визначається робота пружної сили.

16. Запишіть формули силової функції сили тяжіння, пружної сили.

17. Як визначається елементарна робота системи сил, прикладеної до механічної системи? Запишіть формулу визначення цієї елементарної роботи в проекціях на координатні осі.

18. Чому дорівнює елементарна робота внутрішніх сил незмінюваної системи?

19. Якою є елементарна робота в системі матеріальних точок, що змінюється?

20. Як визначається робота сили ваги в системі матеріальних точок?

21. Як обчислити елементарну роботу сил, прикладених до твердого тіла, при його поступальному русі, при обертальному русі і при плоскому русі?

22. Як визначається і що характеризує потужність?

23. Запишіть формулу визначення потужності сили, прикладеної до матеріальної точки.

24. Як визначити потужність крутного моменту?

25. В яких одиницях вимірюється потужність в системі СІ?

26. Сформулюйте послідовність розв’язання задачі на визначення сумарної роботи сил, прикладених до матеріальної точки або до системи матеріальних точок.

27. Сформулюйте теорему про зміну кінетичної енергії матеріальної точки на нескінченно малому переміщенні і на даному відрізку шляху точки.

28. Запишіть формулу, яка виражає теорему про зміну кінетичної енергії матеріальної точки.

29. Що називають силовим полем?

30. Яке силове поле називають стаціонарним?

31. Яке стаціонарне силове поле називають потенціальним?

32. Наведіть приклади потенціальних силових полів.

33. Чим визначається потенціальна енергія в даному положенні матеріальної точки?

34. Як виражається елементарна робота сили потенціального поля?

35. Яку величину має повна механічна енергія при русі матеріальної точки в потенціальному силовому полі?

36. Що називають повною механічною енергією матеріальної точки?

37. Сформулюйте порядок розв’язання задач за допомогою теореми про зміну кінетичної енергії матеріальної точки.