Теорема про змiну моменту кiлькостi руху матерiальної точки. Закон збереження моменту кiлькостi руху матерiальної точки

Моментом кiлькостi руху матерiальної точки М маси m вiдносно даного центра О називають вектор

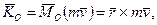(9.33)

що є векторним добутком радiуса-вектора 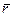= 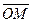та кiлькості руху 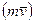цiєї точки.

Теорема про змiну момента кiлькостi руху: похiдна за часом вiд моменту кiлькостi руху матерiальної точки, взятого вiдносно нерухомої точки простору, дорiвнює моменту діючої сили вiдносно тiєї ж самої точки простору:

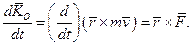(9.34)

Вектор 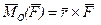напрямлений по перпендикуляру до площини, в якiй в даний момент лежать сила 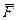i центр О, вектор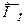 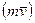- по перпендикуляру до площини, в якiй лежать кiлькiсть руху 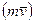i центр О (рис. 9.3).

Величина вектора M_O 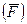дорiвнює:

M_O 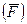= F×H, (9.35)

де Н - довжина перпендикуляра, проведеного з точки О на напрям сили .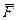

Величина вектора M_O 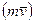дорiвнює:

M_O(m 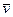) = mvh, (9.36)

де h - довжина перпендикуляра, проведеного з центру О на напрям вектора .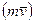

Швидкiсть змiни вектора 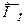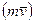дорiвнює вектору .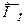

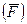Як завжди, векторна рiвнiсть (9.34) еквiвалентна до трьох скалярних рівнянь:

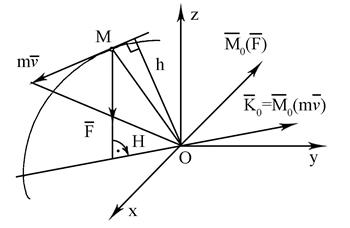
Рис. 9. 3.

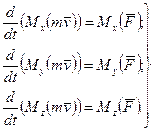(9.37)

Кожна з трьох рiвностей виражає теорему моментiв вiдносно осi: похiдна за часом вiд моменту кiлькостi руху матерiальної точки вiдносно нерухомої осi дорiвнює моменту сили, що дiє на точку, вiдносно цiєї ж осi.

У розгорнутому виглядi рiвняння (9.37) мають вигляд:

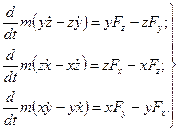(9.38)

Тут х, у, z - координати рухомої точки, F_x, F_y, F_z - проекцiї прикладеної до точки сили на вісі x, y, z.

Закон збереження моменту кiлькостi руху матерiальної точки:

а) якщо момент прикладеної до матерiальної точки сили вiдносно нерухомого центра дорiвнює нулю, то момент кiлькостi руху точки вiдносно того ж центра зберiгає незмiнними величину i напрям.

Справдi, при умовi 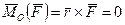з рiвностi (9.34) маємо

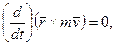
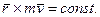
Оскiльки m = соnst , то 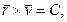тобто в даному випадку момент швидкостi є сталою величиною;

б) якщо момент прикладеної до точки сили відносно нерухомої осі дорiвнює нулю, то момент кiлькостi руху матерiальної точки вiдносно тiєї ж осi зберiгає незмiнну величину.

При розв’язуваннi задач на застосування теореми про змiну моменту кiлькостi руху матерiальної точки доцiльно дотримуватись такого порядку:

1) вибрати систему координат. Якщо точка рухається по дузi кола, то одну з осей слiд направити через центр кола, а другу вiсь вибрати дотичною до кола;

2) показати на рисунку сили, прикладенi до матерiальної точки, тобто активнi сили i сили реакцiй в’язей;

3) обчислити суми моментiв сил, прикладених до матерiальної точки, вiдносно осей координат;

4) показати на рисунку вектор кiлькостi руху матерiальної точки, записати вираз моментiв кiлькостi руху вiдносно осей координат i взяти вiд них похiдні за часом;

5) скласти рiвняння теореми про змiну моменту кiлькостi руху матерiальної точки;

6) визначити згiдно умови задачi необхiднi величини.

Питання для самоконтролю

1. Який вектор називають моментом кількості руху матеріальної точки відносно даного центра?

2. Сформулюйте та запишіть теорему про зміну моменту кількості руху матеріальної точки.

3. Які напрями і величини мають вектори моментів сили 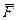та кількості руху 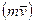відносно центра О?

4. Чому дорівнює швидкість зміни вектора моменту кількості руху матеріальної точки?

5. Запишіть теорему про зміну моменту кількості руху матеріальної точки в проекціях на осі декартових координат. Що виражають ці рівняння?

6. Запишіть рівняння теореми про зміну моменту кількості руху точки в проекціях на координатні вісі в розгорнутому вигляді.

7. Сформулюйте два випадки проявлення закону збереження моменту кількості руху матеріальної точки.

8. Яка методика розв’язання задач на застосування теореми про зміну моменту кількості руху матеріальної точки?