Параметрические уравнения прямой.

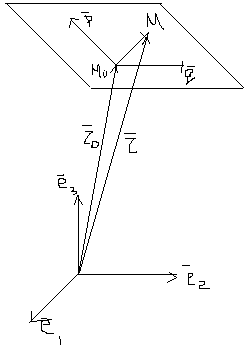
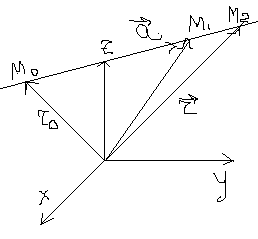Возьмём СК

М- текущая точка на прямой, 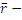текущий вектор, по правилу сложения векторов:

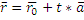- параметрическое уравнение прямой!

t- коэффициент –параметр.

Рассмотрим параметрическое уравнение прямой в координатном виде, тогда получим:

-\

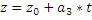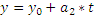- -- параметрическое уравнение прямой в пространстве (в координатном виде)

- /

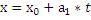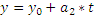-//- на плоскости

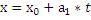
Параметрическое уравнение плоскости в пространстве:

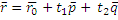
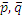- направляющие векторы, 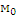- начальная точка плоскости, М- текущая точка плоскости.

Х= 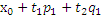параметрическое уравнение плоскости

Y= 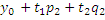в координатном виде

Z=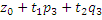

Рассмотрим связь между общими уравнениями прямой и плоскостью и параметрическими уравнениями:

Общие Ах+Ву+Сz+D=0 – уравнение плоскости

Ах+Ву+С=0 -уравнение прямой

1)Для плоскости:

Ах+Ву+Сz+D=0

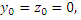таким образом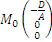

2)аналогично для прямой

Нахождение координат в начальной точке из общего уравнения:

Рассмотрим как найти направляющие косинусы:

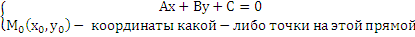
А 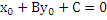вычитаем из первого второе

А(х- 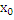)+В(у- 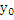)=0

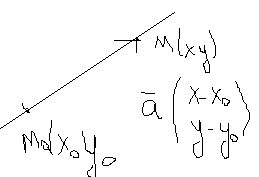Этот вектор параллелен прямой ,когда лежит на этой прямой.