Предложение 1. О направляющем векторе прямой на пл-ти.
Каждый не нулевой вектор 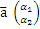 с компонентыми
с компонентыми 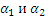 ,которые удовлетворяют уравнению:
,которые удовлетворяют уравнению:
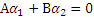 может быть принят за направляющий вектор прямой, определяемый следующим уравнением: Ах+Ву+С=0,
может быть принят за направляющий вектор прямой, определяемый следующим уравнением: Ах+Ву+С=0, 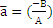 в частности направляющий вектор будет
в частности направляющий вектор будет 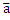
А(х- 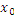 )+В(у-
)+В(у- 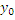 )= 0
)= 0
Параметрические уравнения плоскости.
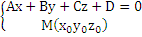 А(х-
А(х- 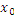 )+В(у-
)+В(у- 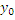 )+С(z-
)+С(z- 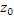 )= 0
)= 0
Предложение 2. О направляющих векторах плоскости.
Любые два неколлинеарных вектора компоненты которых удовлетворяют уравнению:
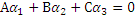 могут быть приняты за направляющие векторы плоскости в общий декартовой системе координат.
могут быть приняты за направляющие векторы плоскости в общий декартовой системе координат.
Исключение параметра из параметрических уравнений прямой.
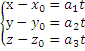 параметрические уравнения прямой на плоскости
параметрические уравнения прямой на плоскости
Определение углового коэффициента прямой.
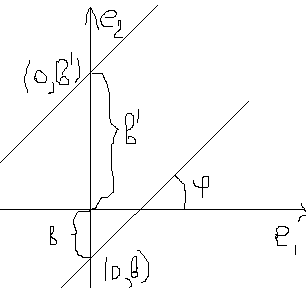
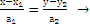
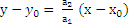 , где к=
, где к=  называется угловым коэффициентом прямой.
называется угловым коэффициентом прямой.
Это означает, что точка с координатами (0,в) лежит на прямой.
Предложение 3 об уравнении прямой.
Если прямая не параллельная оси координат, то есть 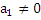 , то ее уравнение: у=Кх+В
, то ее уравнение: у=Кх+В
К-угловой коэффициент, В-точка пересечения с осью У. Из рисунка видно, когда B>0 и когда B<0.
Дата добавления: 2016-07-18; просмотров: 1747;











