Вывод волнового уравнения для электромагнитных волн
Переменное электрическое поле порождает переменное магнитное и наоборот, и это приводит к возникновению электромагнитной волны. Выведем волновое уравнение из I и II уравнений Максвелла в интегральной форме.
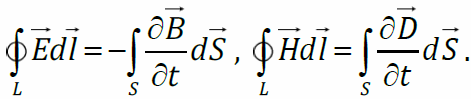
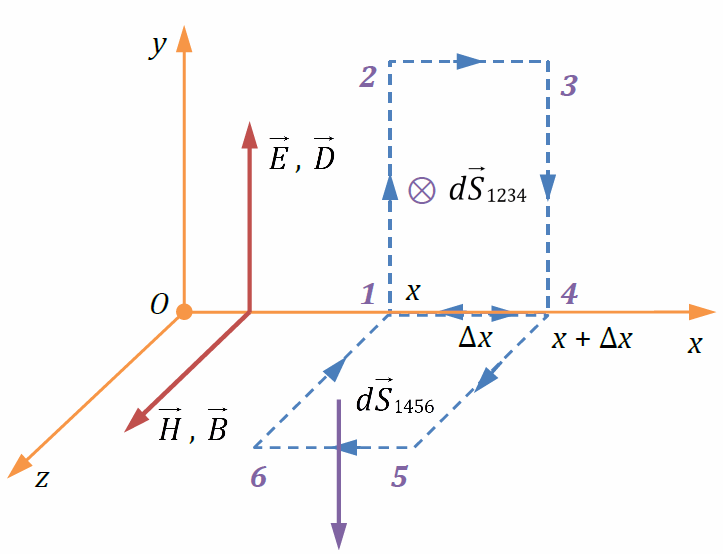 Пусть в пространстве (однородной, изотропной, неферромагнитной среде с относительной электрической и магнитной проницаемостями ε, μ) существует переменное электрическое поле. Свободные заряды и макротоки отсутствуют. Напряжённость электрического поля направлена вдоль оси y и изменяется только вдоль оси x. При этом магнитная индукция будет направлена вдоль оси z:
Пусть в пространстве (однородной, изотропной, неферромагнитной среде с относительной электрической и магнитной проницаемостями ε, μ) существует переменное электрическое поле. Свободные заряды и макротоки отсутствуют. Напряжённость электрического поля направлена вдоль оси y и изменяется только вдоль оси x. При этом магнитная индукция будет направлена вдоль оси z:
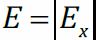 и
и 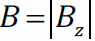
Мысленно выделим в пространстве прямоугольные контуры 1234 в плоскости xyи 1456 в плоскости xz, причём ширина контуров Δx<<x. Циркуляция E по контуру 1234:
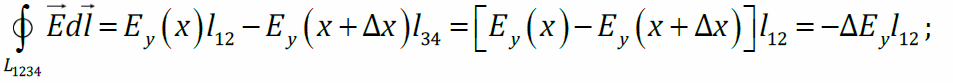
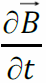 поток сквозь поверхность, натянутую на этот контур, взятый с обратным знаком:
поток сквозь поверхность, натянутую на этот контур, взятый с обратным знаком:
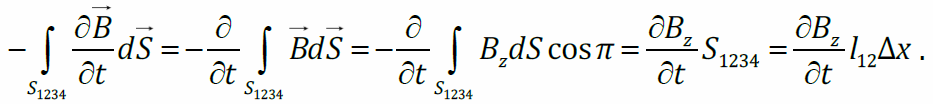 Подставим в I уравнение Максвелла и поделим на Δx:
Подставим в I уравнение Максвелла и поделим на Δx:
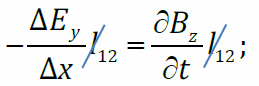 при Δt→ 0
при Δt→ 0 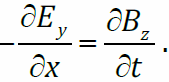
Циркуляция напряжённости магнитного поля по контуру 1456:
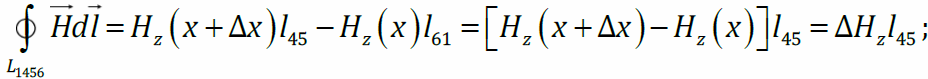
ток смещения сквозь поверхность, натянутую на этот контур,
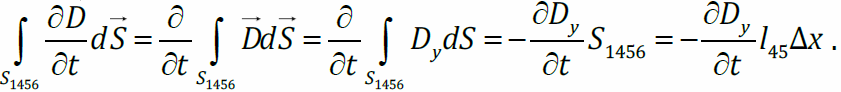 Подставим во II уравнение Максвелла и поделим на Δx:
Подставим во II уравнение Максвелла и поделим на Δx:
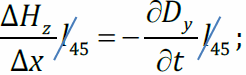 при Δt→ 0
при Δt→ 0 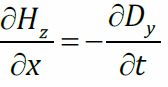 . Т.к.
. Т.к. 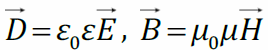
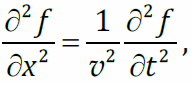

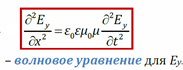
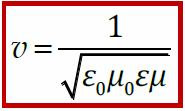
Общий вид волнового уравнения (для плоской волны)
Дата добавления: 2016-07-05; просмотров: 6839;











