Свойство линейности СП.
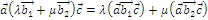
Предложение 6 о линейности ВП.
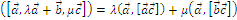 , где
, где 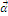 – произвольный вектор.
– произвольный вектор.
Выражение векторного и смешанного произведения через компоненты сомножителей.
Если вместо вектора 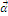 подставить базисно-единичные вектора
подставить базисно-единичные вектора 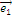 ,
, 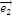 ,
, 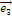 , то получим равенство соответствующих компонентов векторов в формуле (пункт 51).
, то получим равенство соответствующих компонентов векторов в формуле (пункт 51).
Теорема 2 о представлении векторного произведения.
В ортоганальном базисе векторное произведение выражается через компоненты следующим образом:
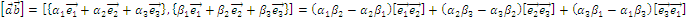
Теорема 3 о представлении смешанного произведения.
Смешанное произведение выражается через компоненты по формуле:
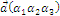 ,
, 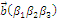 ,
, 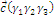 .
.
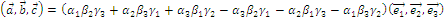 , где
, где 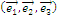 - смешанное произведение базисных векторов.
- смешанное произведение базисных векторов.
Детерминанты, 2-го и третьего порядка в связи с ВП и СмП.
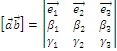 – векторное произведение через детерминант 3-го порядка.
– векторное произведение через детерминант 3-го порядка.
Представление выражения для ВП через Детерминант 2-го порядка.
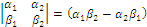 - детерминант 2-го порядка.
- детерминант 2-го порядка.
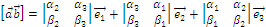 – ВП через детерминант 2-го порядка.
– ВП через детерминант 2-го порядка.
Представление выражения для СмП через Детерминант 3-го порядка.
 - СмП через детерминант 3-го порядка.
- СмП через детерминант 3-го порядка.
Выражение решения системы 3-го порядка через СмП.
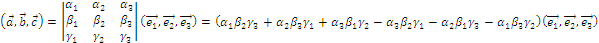
Дата добавления: 2016-07-18; просмотров: 1647;











