Предложение5.О связи векторного и скалярного уравнения плоскости.
Пусть 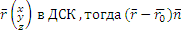 → Ax+By+Cz+D (скалярное произведение) Инаоборот , если имеется такой
→ Ax+By+Cz+D (скалярное произведение) Инаоборот , если имеется такой 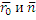 многочлен, то для него можно найти соответственно.
многочлен, то для него можно найти соответственно.
Предложение 6.. О нормальном векторе плоскости.
В ДПСК вектор 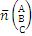 является нормальным вектором для плоскости, определяемой следующим уравнением: Ах+Ву+Сz+D=0. Всё что мы говорили о плоскостях в пространстве, то же самое мы можем сказать о прямых на плоскости.
является нормальным вектором для плоскости, определяемой следующим уравнением: Ах+Ву+Сz+D=0. Всё что мы говорили о плоскостях в пространстве, то же самое мы можем сказать о прямых на плоскости.
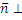 прямой
прямой
( 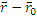 ),
), 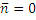 (
( 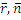 )=C
)=C
Ax+By+C=0
A=( 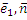 ) , B=(
) , B=( 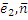 )
)
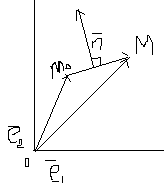
Если в декартовой прямоугольной системе координат вектор 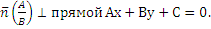
Признаки параллельности плоскостей и прямых на плоскости.
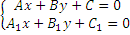 в ДСК
в ДСК
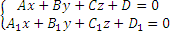
Параллельны тогда и только тогда, когда :
а) 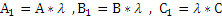
условие совпадения:
б) 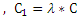 /
/ 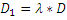
из рассмотрения векторного уравнения прямой пересечения.
Предложение 8.(О прямых на пл-ти ). Признаки параллельности прямых на плоскости.
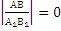
Предложение 9. ( О плоскостях в пр-ве). Признаки параллельности плоскостей.
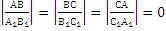
Предложение 10. (О системе 2-х уравнений).
Уравнения прямой в пространстве.
Предложение 11. О направляющем векторе прямой в пространстве.
Вектор с компонентами:
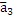 =
= 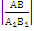 ,
, 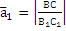 ,
, 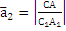
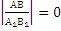
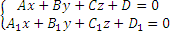
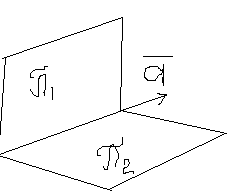 Направляющий вектор прямой, определяемый как пересечение этих двух плоскостей
Направляющий вектор прямой, определяемый как пересечение этих двух плоскостей
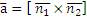
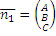 ,
,  =
= 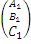
Дата добавления: 2016-07-18; просмотров: 1474;











