Предложение4 об уравнении прямой, параллельной оси ординат.

Если прямая параллельна оси координат, то ее уравнение записывается в виде х= 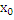, это получается из параметрического уравнения прямых. Исключим параметр T из параметрических уравнений прямой в пространстве:

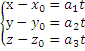
Каноническое уравнение прямой.

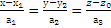это соответствует тому , что прямая есть пересечение двух плоскостей. Эта прямая лежит в плоскости х= .

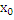Векторные уравнения плоскости и прямой.

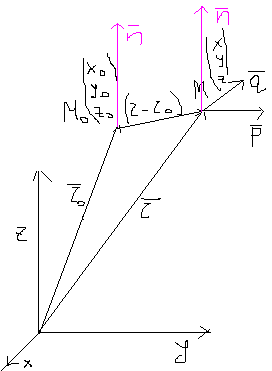Плоскость определяется задание ее начальной точки и вектора 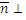этой плоскости.

Условие 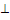двух векторов есть скалярное произведение

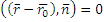условие нахождения произведения точки плоскости 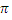, то есть векторное уравнение плоскости.

Рассмотрим вектора 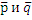, тогда в качестве 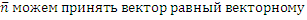произведению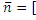

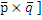
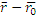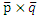(( ),[ ])=0 → (( 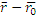) )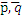=0 → ( 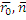)+D=0 → D= - ( )

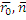Векторные уравнения прямой.

Предложение 7.О нормальном векторе прямой на пл-ти.

Векторные уравнения прямой в пр-ве.

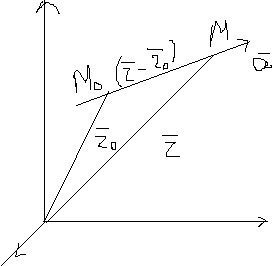условие коллинеарности:

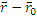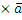[( ) ]=0

↑векторное уравнение, 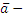направляющий вектор прямой.

Уравнение прямой не содержащее начальную точку:

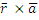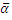[ ] = , начальная точка прямой : 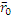=t[ ]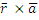

Векторные уравнения плоскости.