Предложение 1 о компонентах вектора в ортонормированном базисе.
Если базисные вектора 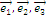 ортогональны (┴), то компоненты любого вектора находятся по формулам:
ортогональны (┴), то компоненты любого вектора находятся по формулам:
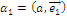 ;
; 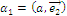 ;
; 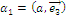 .
.
Предложение 2 о линейности СП.
Свойство линейности СП для любых 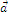 ,
, 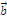 ,
, 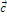 чисел
чисел 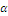 и
и 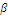 имеет вид:
имеет вид:
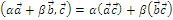
Следствия:
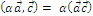
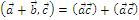
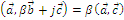
Теорема 1 о представлении СП.
Если базис перпендикулярен, то скалярное произведение векторов вирируется:
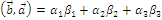
Доказательство:
Пользуясь 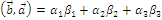 и
и 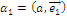 ;
; 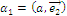 ;
; 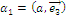 , полученное будем последовательно перемножать (1ую сумму на 2ую).
, полученное будем последовательно перемножать (1ую сумму на 2ую).
s w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="20"/><w:sz-cs w:val="20"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 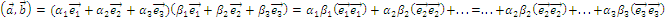
Таким образом и получим выписанное выражение.
Таблица перемножения базисных векторов для СП.
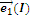
| 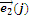
| 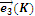
| |
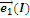
| |||
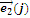
| |||
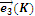
|
Дата добавления: 2016-07-18; просмотров: 1536;











