Деление отрезка в заданном отношении.
Рассмотрим отрезок АВ .
Найдем координаты т.М ,которая делит АВ отрезок в отношении 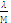
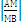 =
= 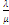
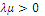
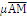 =
=  (1)
(1)
Обозначим через (x , y , z) координаты точки А, ( 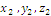 ) –т. В , (
) –т. В , ( 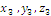 ) –т. М
) –т. М
Разложим обе части равенства (1) по базису, тогда имеем 3 уравнения с 3 неизвестными
 {
{  } - ?
} - ?
формулы деления отрезка в заданном отношении:
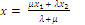
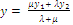

Если одно из выражений будет отрицательным то точки М будет находится в не отрезка АВ.
Соответственно это будет деление отрезка АВ внешним образом.
Декартова прямоугольная система координат.
ДСК, которая имеет нормированный базис называется ДПСК.
Определение ортонормированного базиса.
Базис называется ортонормированным, если его векторы 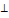 (ортогональны) , а по длине =1
(ортогональны) , а по длине =1
 ,
,  ,
, 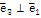 →
→ 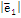 =
= 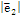 =
= 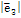 = 1
= 1
Полярная система координат.
Существует формула перехода
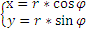 →
→ 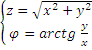
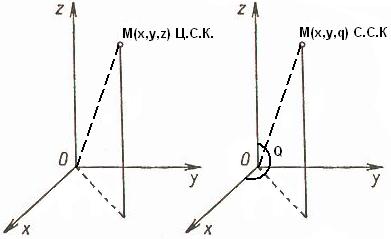
Цилиндрические и сферические координаты.
Определение Скалярного произведения и его свойства.
Скалярное произведение– число, равное произведению двух векторов на косинус угла между ними.
Свойства скалярного произведения:
1.Комунитативность:
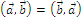
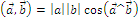
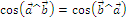
2. 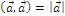 - для любого вектора
- для любого вектора 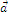
3. 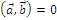 , если
, если 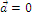 или
или 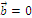 .
.
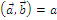 , если
, если 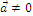 или
или 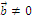 или
или 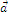 ┴
┴ 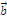 .
.
Дата добавления: 2016-07-18; просмотров: 1864;











