Предложение 8 о 4-х векторах.

Любые четыре вектора линейно-зависимы, любой вектор может быть разложен по трем некомпланарным векторам.

Определение Декартовой системы координат.

Фиксируем в пространстве произвольную точку О и рассмотрим некоторую точку М , тогда радиус-вектор точки М относительно точки О называется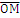

Если в пространстве кроме точки О задан некоторый базис , то точки М можно сопоставить упорядоченную тройку чисел – компоненты ее радиус-вектора.

Декартовой системой координат называется совокупность точки и базиса.

Точка О – начало координат , а прямые , проходящие в направлении базисных векторов, являются осями координат.

Ось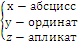

Плоскости , проходящие через координаты оси, называются плоскостям координат.

Определение координат точки.

Компоненты радиус-вектора 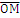называются координатами т. М в рассматриваемой системе координат, координаты т. определяются однозначно.

Предложение 1 о компонентах вектора.

Чтобы найти компоненты вектора нужно из координат конца вычесть координаты начала

М’М (х’-x, y’-y, z’-z)