Линейная зависимость векторов.

Линейная комбинация векторов называется тривиальной, если все ее коэффициенты равны нулю.

Линейная комбинация векторов называется не тривиальна, если хотя бы один из её коэффициентов отличен от нуля.

Определение о линейной зависимости векторов.

Векторы 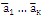называются линейнозависимые , если существует нетривиальная линейная комбинация этих векторов равная нулю:

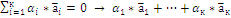= 0 , где 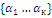– линейнозависимые

В противном случае эти вектора называются линейно-независимыми , т.е. сумма

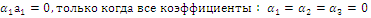тогда, когда .

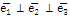Предложение 5 о линейной зависимости системы векторов.

Система векторов линейно-зависима тогда и только тогда , когда один из них раскладывается в линейную комбинацию остальных.

Доказательство:

= 0

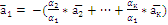
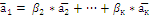
Предложение 6 о коллинеарных векторах.

Любые два коллинеарных вектора линейнозависимы. Два линейнзависимых вектора коллинеарны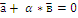

24. Предложение 7 о 3-х компланарных векторах.

Любые три компланарных вектора линейно-зависимы и наоборот.

На плоскости любой вектор можно разложить по двум векторам.