Линейные комбинации векторов.

Применяя линейные операции мы можем составлять суммы векторов умноженных на число:

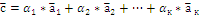
Сумма векторов умноженных на число называется линейные комбинация этих векторов.

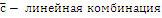
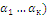( - коэффициенты линейной комбинации векторов

Пользуясь свойствами линейной комбинации можно производить над векторами разные преобразования.

Свойства линейной комбинации:

1. Если все { 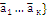- коллинеарны, то и их линейный комбинации коллинеарны.

2. Если стационарны, то линейные комбинации стационарны.

Определение базиса.

1. Базисв пространстве ,называются три некомпланарные вектора

2. На плоскости два неколлинеарных вектора

3. На прямой один не нулевой вектор

Если вектор представлен как линейная комбинация, то говорят что он разложен по этим векторам. Обычно рассматривается разложение вектора по базисам.

Определение компонент векторов.

Если 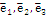есть базис в пространстве и вектор 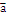представлен как:
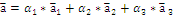(линейная комбинация )

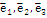Тогда числа { 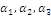} называются компоненты (координаты) вектора 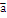в данном базисе.