Приклади обчислення робіт

1. Робота сили тяжіння.

Знайдемо роботу сили тяжіння 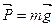при переміщенні точки із положення 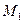в положення 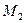по довільній траєкторії (рис.2.18). Оберемо координатний спосіб обчислення роботи. Направимо вісь Oz вертикально вниз, а осі Ox і Oy розташуємо у горизонтальній площині.

Тоді X = Y = 0 ; Z = mg . (i)

Підставивши (i) у формулу (2.18) , отримаємо

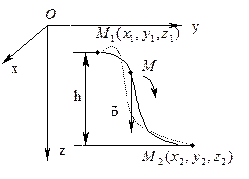
рис.2.18

.

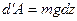Отже, елементарна робота залежить тільки від координати z, тому при обчисленні роботи за формулою (2.19) криволінійний інтеграл заміниться визначеним із границями інтегрування 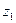і :

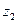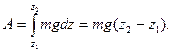(j)

Різниця 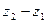визначає переміщення точки по вертикалі , яку позначимо ± h .Тоді формула (j) матиме вигляд

A=±mgh. (2.21)

Додатній знак у формулі (2.21) відповідає вертикальному переміщенню, що співпадає з напрямом сили тяжіння 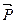, від’ємний – тому випадку, коли вертикальні переміщення і сила тяжіння 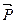направлені в протилежні сторони.

Із формули (2.21) видно, що робота сили тяжіння залежить не від форми траєкторії точки, а тільки від переміщення точки по вертикалі .

2. Виведемо формулу для роботи, що створюється центральною силою.

Центральною називається сила, лінія дії якої постійно проходить через деяку фіксовану точку – центр притягання або відштовхування.

Величина центральної сили пропорційна відстані точки до центру притягання або відштовхування. Як приклад центральної сили можна привести сили всесвітнього тяжіння, кулонівські сили притягання або відштовхування, сили пружності та ін.

Припустимо, що матеріальна точка M рухається під дією центральної сили (рис.2.19).

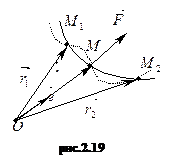
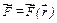, де r – відстань точки до центра відштовхування. Введемо одиничний вектор

.

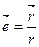Тоді 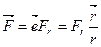. (k)

Тут 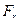– проекція сили 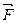на напрям вектора 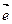. 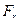<0 для сили притягання, 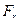>0 для сили відштовхування. Підставивши (k) у (g), отримаємо

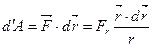. (l)

Взявши до уваги, що 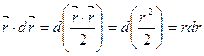, знайдемо формулу для отримання елементарної роботи , що здійснюється центральною силою :

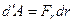. (2.22)

Знайдемо повну роботу, що здійснюється центральною силою, приймаючи до уваги, що :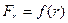

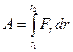, (2.23)

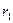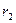де і – початкова і кінцева відстань точки М до центра притягання або відштовхування .

Як видно із (2.23), результат інтегрування не залежить від того, вздовж якої прямої рухається точка. Отже, робота, що здійснюється центральною силою, залежить не від форми траєкторії точки, а від її початкового і кінцевого положення.

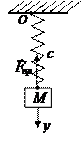
рис. 2.20

3. Застосуємо формулу (2.23) для обчислення роботи, що здійснюється силою пружності.

Матеріальна точка М, з’єднана пружиною із нерухомим шарніром в точці О (рис.2.20). Припустимо, що матеріал пружини підлягає закону Гука і вона розтягнута. На точку М уздовж осі пружини діє сила пружності, направлена до шарніру, при цьому

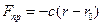, (m)

де с- жорсткість пружини, r і 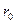– довжина деформованої і недеформованої пружини відповідно.

Підставивши (m) у (2.23), отримаємо

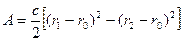. (2.24)